Classes assintóticas

Antes de ler este artigo é necessário que você já tenha lido o artigo sobre comportamento assintótico. Se você ainda não leu, clique aqui.

Vimos no último artigo a importância da identificação do comportamento assintótico para o processo de análise de algoritmos. Neste artigo vamos conhecer as classes assintóticas. Classes que a ciência da computação utiliza para classificar os algoritmos de acordo com o seu desempenho.

Introdução às classes assintóticas de algoritmos

Foi mostrado que a função de complexidade T(n) de um algoritmo fornece poucos detalhes a respeito da sua eficiência. Entretanto, a análise gráfica do seu comportamento assintótico consegue mostrar com maior precisão como se comporta o seu desempenho durante a sua execução.

O segredo do comportamento assintótico de um algoritmo está no termo polinomial de maior grau da sua função de complexidade, pois esse termo define a sua classe assintótica. Veja abaixo:

No algoritmo:

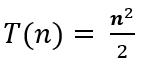
O que realmente importa é o termo de maior grau, o n². Portanto, é um algoritmo de classe quadrática.

No algoritmo:

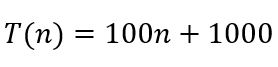
O que realmente importa é o termo de maior grau, o n. Portanto, é um algoritmo de classe linear.

No algoritmo:

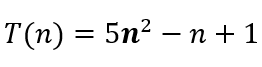
O que realmente importa é o termo de maior grau, o n². Portanto, é um algoritmo de classe quadrática.

No algoritmo:

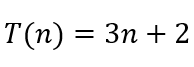
O que realmente importa é o termo de maior grau, o n. Portanto, é um algoritmo de classe linear.

No algoritmo:

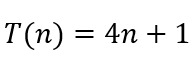
O que realmente importa é o termo de maior grau, o n. Portanto, é um algoritmo de classe linear.

Veja abaixo uma lista com as classes assintóticas mais comuns existentes em análise de algoritmos.

n!

Fatorial

A pior classe existente. Geralmente ocorre em alguns algoritmos que usam a técnica de força bruta para resolver problemas.

2ⁿ

Exponencial

Mais eficiente que o fatorial, porém ainda muito longe de ser um algoritmo eficiente. Também ocorre em algoritmos que usam força bruta para resolver problemas.

n^k

Polinomial

São mais eficientes que os exponenciais, porém só são adequados para resolver pequenos problemas. Quando o valor de n cresce muito, o algoritmo se torna bastante ineficiente.

n²

Quadrática

Polinomiais de ordem quadrática. Essa classe ocorre bastante em algoritmos que processam informações aos pares. Geralmente em loops aninhados (um loop dentro do outro).

n log n

Linear logarítmica

Um pouco menos eficientes que os lineares. Essa é uma classe assintótica típica dos algoritmos que implementam o paradigma de “divisão e conquista”.

n

Linear

Algoritmo muito eficiente. A classe linear ocorre em algoritmos que precisam processar n elementos de entrada e fazer pequenas computações sobre esses elementos.

log n

Logarítmica

O melhor dos mundos para os algoritmos. Essa classe é típica de algoritmos que podem resolver os problemas transformando-os em problemas menores a cada etapa da resolução.

1

Constante

O nirvana dos algoritmos. Na verdade, esta é uma situação muito improvável, pois ocorre em algoritmos que não realizam nenhuma computação significativa e, portanto, não possuem muita utilidade.

Diferença de eficiência em uma mesma classe

E se dois algoritmos forem da mesma classe assintótica? Qual será o mais eficiente?

Dois algoritmos pertencentes a uma mesma classe possuem o mesmo comportamento assintótico. Isso significa que: as pequenas variações de desempenho entre algoritmos de uma mesma classe não possuem grande importância.

Vejamos o porquê:

Imagine dois algoritmos C e D, ambos de classe linear:

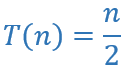
Algoritmo C

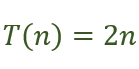
Algoritmo D

Abaixo, segue a tabela com a quantidade de instruções realizadas pelos algoritmos para os valores iniciais de n. Percebe-se que o algoritmo C é mais eficiente que o D, apesar de ambos serem da mesma classe assintótica (a classe linear).

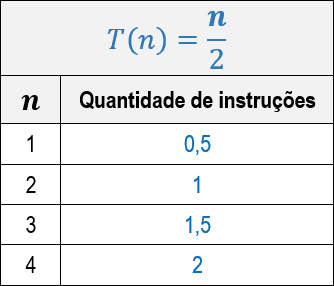
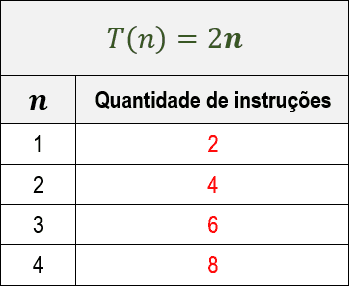
Independente do fato do algoritmo C ser mais eficiente do que o D, essa diferença entre as eficiências nunca se propagará. Observe nos gráficos ilustrados abaixo como a diferença de eficiência entre ambos sempre permanecerá constante para valores diferentes de n.

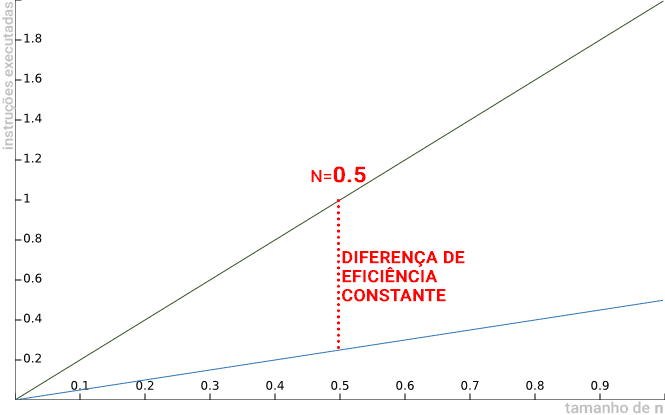
Perceba que, independente de quão grande for o valor de n, a diferença de eficiência entre os algoritmos de uma mesma classe assintótica sempre permanecerá constante. Por este motivo, as constantes aditivas e multiplicativas da fórmula de complexidade não são importantes para a análise. Em algoritmos pertencentes a uma mesma classe, o desempenho será muito parecido para grandes valores de n(n→∞).

Desta forma, fica claro que, para a análise de algoritmos, o que importa é apenas definir a classe do algoritmo, pois ela define o seu comportamento assintótico.

Diferença de eficiência em classes distintas

Em algoritmos de classes assintóticas distintas, a diferença de eficiência se propagará ao passo que o valor de n cresce. Considere os dois algoritmos E(classe quadrática) e F(classe linear):

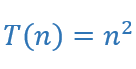
Algoritmo E

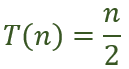
Algoritmo F

Abaixo, segue a tabela com a quantidade de instruções realizadas pelos algoritmos para os valores iniciais de n. Percebe-se que o algoritmo F é mais eficiente que o E.

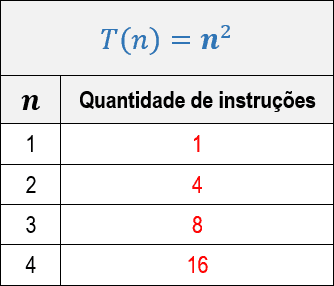
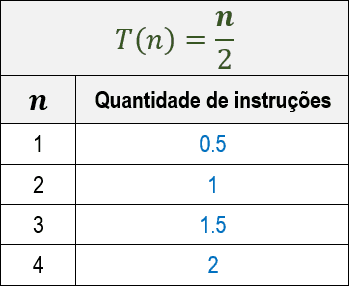
O interessante de ser observado aqui é que essa diferença de eficiência entre os algoritmos se propaga ao passo que o valor de n cresce, pois trata-se de dois algoritmos de classes assintóticas distintas. Observe nos gráficos ilustrados abaixo como a diferença de eficiência entre ambos se propaga para valores diferentes de n.

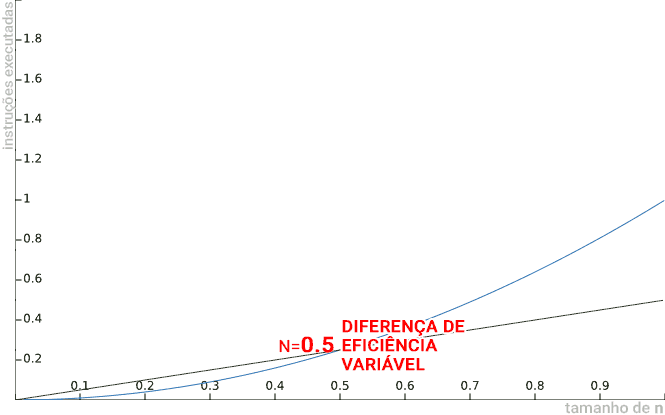
Perceba que, ao passo que o valor de n cresce, a diferença de eficiência entre os algoritmos fica cada vez mais acentuada. Portanto, fica clara a importância das classes assintóticas para o processo de análise. Em algoritmos pertencentes à classes distintas, o desempenho sofrerá muito impacto para grandes valores de n(n→∞).

Agora que você aprendeu os conceitos de comportamento e classes assintóticas, você pode começar a compreender as notações assitóticas utilizadas para representar o desempenho dos algoritmos na ciência da computação.

Clique neste link e prossiga com o aprendizado da primeira notação: a notação Big O.