Notação Theta

No último artigo conhecemos a segunda notação computacional utilizada para definir o comportamento assintótico dos algoritmos: a notação Ω (Ômega). Neste artigo te ensinaremos a terceira notação computacional utilizada para definir matematicamente o comportamento assintótico de algoritmos: a notação Theta, representada pela letra grega Θ.

Se você ainda não leu o artigo sobre a notação Ω (Ômega), clique neste link e acesse o artigo onde explicamos detalhadamente sobre o assunto. É altamente recomendado que você tenha algum conhecimento sobre as notações Big O e Ω (Ômega) antes de ler este artigo!

Da maneira mais objetiva possível, a notação Θ (Theta) nos fornece uma simbologia simplificada para representar um limite justo de desempenho para um algoritmo. Um limite exato de tempo que um algoritmo leva para ser executado.

Ou seja, a notação Θ representa o ponto de encontro entre as notações Ω (limite inferior) e Big O (limite superior).

Definição matemática formal

Diferentemente do que fizemos para os artigos sobre as notações Ω e Big O, vamos abordar a definição matemática da notação Θ antes de partirmos para os exemplos.

Dada duas funções de complexidade de tempo de algoritmos: f(n) e g(n). A definição matemática formal estabelece que:

• f(n) = Θ(g(n)) (lê-se “f de n é Téta de g de n”) se existirem duas constantes positivas c₁ e c₂ e um valor n₀, tais que c₁.g(n) ≤ f(n) ≤ c₂.g(n) para todos os n ≥ n₀

Ou seja, se ele for limitado superiormente e inferiormente (ao mesmo tempo) pela mesma função g(n).

Vamos demonstrar com alguns exemplos ilustrados.

Resolução matemática: 1º exemplo

Vamos tentar demonstrar pela definição que 4n+1=Θ(n) (lê-se “é téta de n”).

Primeiramente, temos que:

• f(n) = 4n+1
• g(n) = n

Se, pela definição matemática, precisamos demonstrar que existem duas constantes positivas c₁ e c₂ e um valor n₀ inicial, de forma que:

• c₁.g(n) ≤ f(n) ≤ c₂.g(n) para todos os n ≥ n₀

Então, para este problema, precisamos mostrar que:

• c₁.n ≤ 4n+1 ≤ c₂.n para todos os n ≥ n₀.

Em resumo: precisamos provar que, para todos os valores de n maiores ou igual a n₀, a função 4n+1 é:

• maior ou igual a c₁ multiplicado por n e;
• menor ou igual a c₂ multiplicado por n.

Para tanto, a primeira decisão que precisamos tomar é escolher valores para as constantes c₁ e c₂. Neste caso, vamos considerar c₁ sendo igual ao valor 4 e c₂ sendo igual ao valor 5. Observe abaixo uma tabela que mostra os resultados da desigualdade para alguns valores de n:

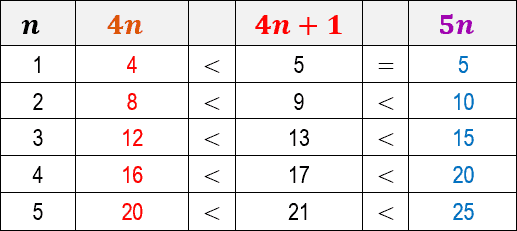
Observe que, para todos os valores de n ≥ 1 expressos na tabela acima, a função do algoritmo 4n+1 é sempre maior que 4n e menor ou igual a 5n.

Quando plotamos um gráfico para ambas as funções, visualizamos com maior clareza como a função 4n+1 é limitada superiormente pela função 5n e inferiormente pela função 4n:

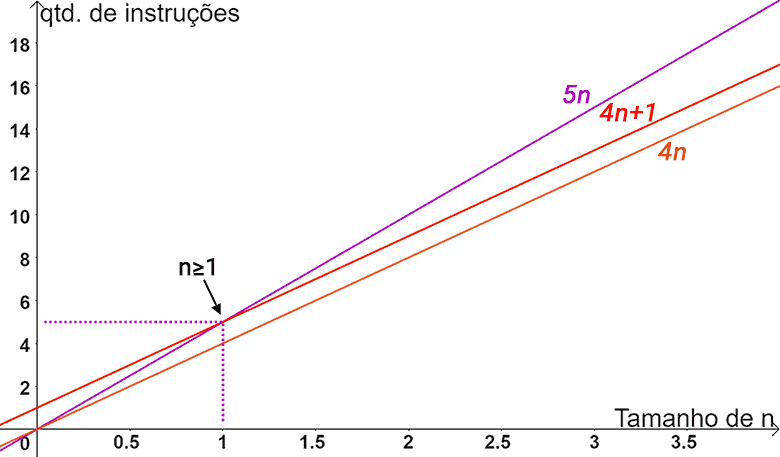
Isso significa que a função 4n+1 nunca terá um comportamento de crescimento inferior a 4n e nem crescerá mais que 5n. Por este motivo, dizemos que Θ(n) representa um limite assintótico justo para a função 4n+1, porque ela é limitada superiormente e inferiormente por duas outras funções de uma mesma classe assintótica que ela: a classe linear n.

Desta forma, conseguimos provar o nosso objetivo. Existem duas constantes positivas c₁=4 e c₂=5 e um n₀=1, tal que c₁.n ≤ 4n+1 ≤ c₂.n para todos os valores de n maiores ou igual a n₀.

Portanto, está provado que, de fato, 4n+1 = Θ(n).

Resolução matemática: 2º exemplo (errado)

Vamos tentar demonstrar pela definição que 5n²-n+1=Θ(n) (lê-se “é téta de n”).

Primeiramente, temos que:

• f(n) = 5n²-n+1
• g(n) = n

Então, para este problema, precisamos mostrar que:

• c₁.n ≤ 5n²-n+1 ≤ c₂.n para todos os n ≥ n₀

Em resumo: precisamos provar que, para todos os valores de n maiores ou igual a n₀, a função 5n²-n+1 é:

• maior ou igual a c₁ multiplicado por n e;
• menor ou igual a c₂ multiplicado por n.

Para tanto, a primeira decisão que precisamos tomar é escolher valores para as constantes c₁ e c₂. Neste caso, vamos considerar c₁ sendo igual ao valor 5 e c₂ sendo igual ao valor 10. Observe abaixo uma tabela que mostra os resultados da desigualdade para alguns valores de n:

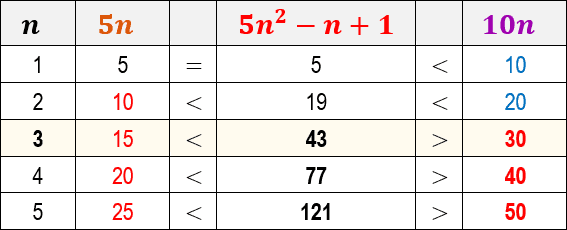
Observe que, para todos os valores de n ≤ 2 expressos na tabela, a função do algoritmo 5n²-n+1 é de fato menor ou igual à função 10n. Contudo, a partir do valor de n=3 a função 5n²-n+1 é supera a função 10n (corrompendo a regra f(n) ≤ c₂.g(n)).

Isso acontece porque a função 10n, sendo linear, nunca conseguirá superar a função 5n²-n+1, que é quadrática.

Veja no gráfico abaixo o relacionamento entre as funções. Podemos visualizar com maior clareza como a função 5n²-n+1 limita inferiormente a função 5n, para valores de n ≥ 1. Contudo, perceba que a função 10n não representa um limite assintótico superior para a função 5n²-n+1, sendo superada por ela para valores de n > 2.

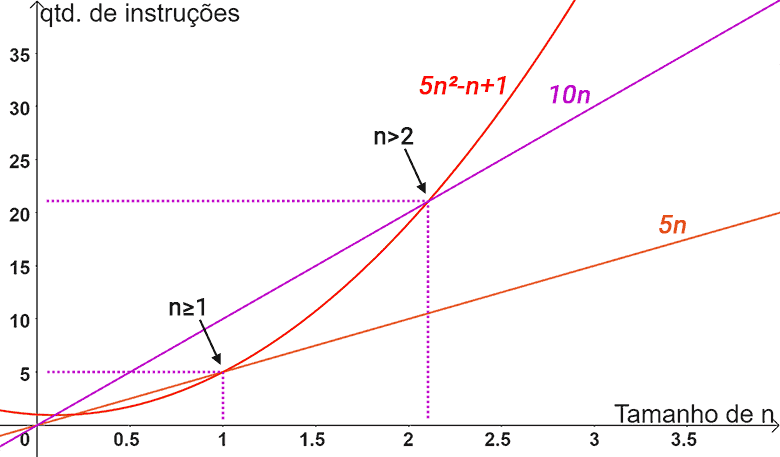
Isso significa que Θ(n) não representa um limite assintótico justo para a função 5n²-n+1. Significa que não existem constantes c₁ e c₂ positivas e um n₀, tal que c₁.n ≤ 5n²-n+1 ≤ c₂.n para todos os valores de n maiores ou igual a n₀.

Desta forma, está provado que, de fato, 5n²-n+1≠Θ(n). (lê-se “não é téta de n”).

Resolução matemática: 3º exemplo (errado)

Vamos tentar demonstrar pela definição que 4n+4=Θ(n²) (lê-se “é téta de n”).

Primeiramente, temos que:

• f(n) = 4n+4
• g(n) = n²

Então, para este problema, precisamos mostrar que:

• c₁.n² ≤ 4n+4 ≤ c₂.n² para todos os n ≥ n₀

Em resumo: precisamos provar que, para todos os valores de n maiores ou igual a n₀, a função 4n+4 é:

• maior ou igual a c₁ multiplicado por n² e;
• menor ou igual a c₂ multiplicado por n².

Para tanto, a primeira decisão que precisamos tomar é escolher valores para as constantes c₁ e c₂. Neste caso, vamos considerar c₁ sendo igual ao valor 1 e c₂ sendo igual ao valor 3. Observe abaixo uma tabela que mostra os resultados da desigualdade para alguns valores de n:

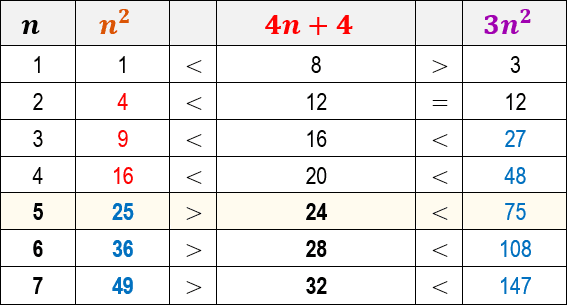
Observe que, para todos os valores de n ≤ 4 expressos na tabela, a função do algoritmo 4n+4 é de fato maior ou igual à função n². Contudo, a partir do valor de n=5 a função 4n+4 é superada pala função n² (corrompendo a regra c₁.g(n) ≤ f(n)).

Acontece que a função n², sendo quadrática, nunca conseguirá ser superada pela função 4n+4, que é linear.

Veja no gráfico abaixo o relacionamento entre as funções. Perceba como a função 4n+4 é superada pelas duas funções (n² e 3n²) para valores de n > 4.

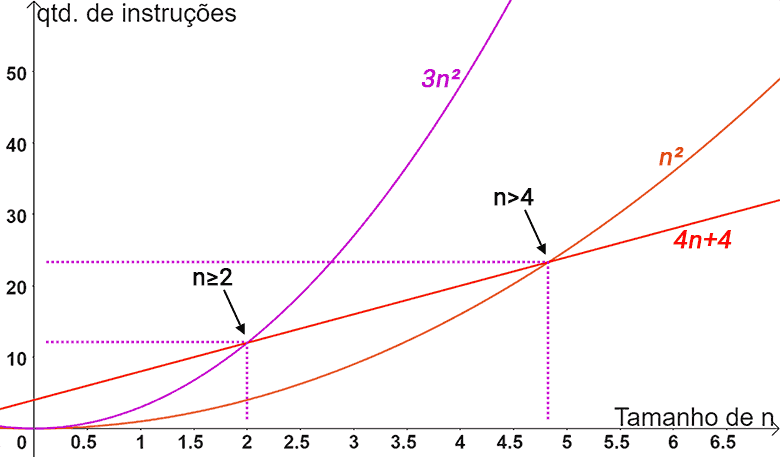
Isso significa que Θ(n²) não representa um limite assintótico justo para a função 4n+4. Significa que não existem constantes c₁ e c₂ positivas e um n₀, tal que c₁.n² ≤ 4n+4 ≤ c₂.n² para todos os valores de n maiores ou igual a n₀.

Desta forma, está provado que, de fato, 4n+4≠Θ(n²). (lê-se “não é téta de n ao quadrado”).

Relações entre as notações Big O, Ômega e Theta

Uma maneira fácil e prática de entender a relação entre as três notações assintóticas (Big O, Ω e Θ) é determinar os limites assintóticos de uma determinada função por meio da construção do que chamamos de tabela assintótica de relacionamento. Veja como ela pode ser feita.

Dada uma função de complexidade de tempo T(n) = 4n+4, podemos facilmente descobrir todas as suas relações Big O, Ω e Θ construindo uma tabela onde as linhas representam as classes assintóticas e as colunas representam as notações.

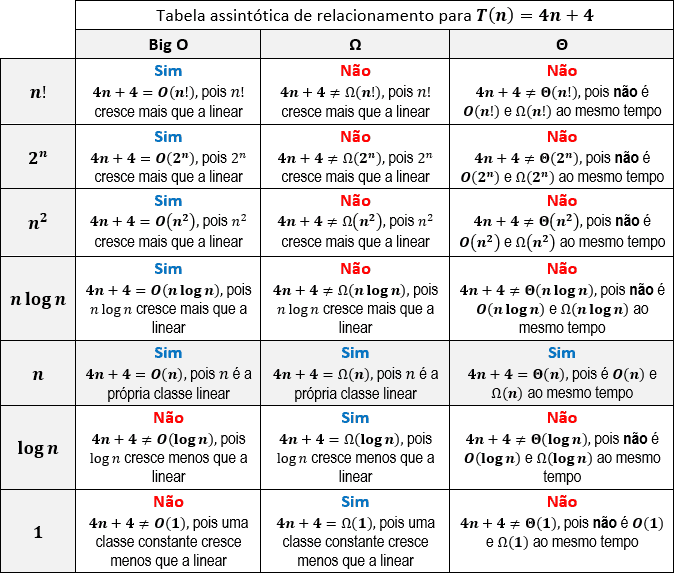
Perceba que uma função T(n) = 4n+4 somente é Θ(n) (Theta de n) pois é Ω(n) (Ômega de n) e O(n) (Big O de n) ao mesmo tempo. Ou seja, uma função é Theta de uma classe se for Ômega e Big O dessa mesma classe assintótica!

Desta forma, entende-se o significado das notações assintóticas Big O, Ω e Θ. Elas servem para representar limites de desempenho de algoritmos.

Limites rígidos e limites frouxos

Os conceitos de limite rígido e frouxo nos permite classificar o desempenho geral de um algoritmo, levando em consideração o seu melhor e pior caso.

Limite assintótico frouxo

Quando afirmamos que o algoritmo A possui:

• No pior caso: T(n) = 5n²-n+1
• No melhor caso: T(n) = 3n+2

Estamos afirmando que:

• No pior caso: T(n) = Θ(n²) (Theta de n ao quadrado), pois possui complexidade quadrática
• No melhor caso: T(n) = Θ(n) (Theta de n), pois possui complexidade linear

Isso significa que o algoritmo A possui um limite assintótico frouxo, visto que, no geral, o seu desempenho se comporta de forma distinta para o melhor e pior caso.

Ou seja, ele, no geral, é O(n²) e Ω(n).

Limite assintótico rígido

Quando afirmamos que o algoritmo B possui:

• No pior caso: T(n) = 4n+1
• No melhor caso: T(n) = 3n+2

Estamos afirmando que:

• No pior caso: T(n) = Θ(n) (téta de n), pois possui complexidade linear
• No melhor caso: T(n) = Θ(n) (téta de n), pois possui complexidade linear

Isso significa que o algoritmo B possui um limite assintótico rígido, visto que, no geral, o seu desempenho se comporta da mesma forma para o melhor e pior caso.

Ou seja, ele, no geral, é Θ(n).

Exercícios

Para demonstrar que você compreendeu bem o conceito e a definição matemática formal da notação Theta, resolva os exercícios propostos:

Exercícios A

Tente demonstrar matematicamente que n²+800 = Θ(n²).

Tente demonstrar matematicamente que n+10 = Θ(n²).

Tente demonstrar matematicamente que 2n+10 = Θ(n).

Tente demonstrar matematicamente que 7n-2 = Θ(1).

Tente demonstrar matematicamente que n²+20n+5 = Θ(n³).

Exercício B

Preencha a tabela assintótica de relacionamento abaixo:

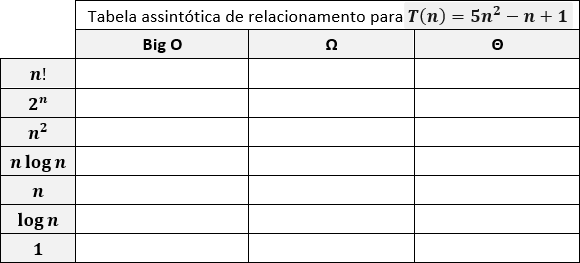
Exercício C

Utilizando a técnica de contagem de etapas, encontre a fórmula de complexidade T(n) do algoritmo abaixo e, em seguida, tente demonstrar matematicamente que essa fórmula encontrada é Θ(n²).

1.public static void func(int[ ] n){
2.    for (int i=0; i<n.length-1; i++) {
3.        for (int j=0; j<n.length-1; j++) {
4.            n[j]=n[j]+(i*j);
5.        }
6.    }
7.}

E assim chegamos ao fim da primeira parte do curso de análise de algoritmos, que teve como objetivo te ensinar os conceitos básicos da técnica de contagem de etapas e as 3 principais notações assintóticas.

Em breve estaramos produzindo a segunda parte deste curso, voltada a ensinar as técnicas utilizadas para a análise dos algoritmos recursivos.