Análise de algoritmos: como se faz?

A análise de algoritmos é uma importante disciplina da Ciência da Computação. Ela tem o objetivo de fornecer métodos mais assertivos para medir o desempenho de algoritmos ou, como se denomina, a sua complexidade de tempo. Esta atividade é de fundamental importância para todo programador ou analista de sistemas, porque ela fornece meios de:

• projetar algoritmos mais eficientes;
• julgar e escolher algoritmos eficientes.

Neste artigo serão abordados os conceitos iniciais sobre a disciplina de análise de algoritmos.

Você vai compreender:

• o que origina a necessidade deste tipo de análise;
• o “modelo analítico” para determinar a complexidade de tempo de um algoritmo;
• a “definição matemática formal” para análise de algoritmos.

IMPORTANTE!

Antes de começar a estudar sobre análise de algoritmos é fundamental que você já conheça os conceitos de “declarações condicionais” e “estrutura de repetição”, que são conceitos básico de programação de computadores.

Bons estudos!

Uma tentativa empírica de análise

A análise de algoritmos pode ser realizada facilmente por métodos empíricos (baseados em experiências práticas), tal como a medição de tempo em segundos que o algoritmo demora para processar uma entrada. Você poderia medir o tempo decorrido antes e depois da execução de um algoritmo e, com base nesse resultado, inferir sobre o seu desempenho.

O código abaixo ilustra um exemplo (usando a linguagem Java) dessa forma empírica de calcular complexidade de tempo. Ele mede o tempo de execução do algoritmo que calcula o n-ésimo termo da sequência de Fibonacci (linhas 15-19).

1.public static void main(String[] args) {
2.        int n;
3.        long start, end;
4.        double cpu_time_used;
5.        Scanner sc = new Scanner(System.in);
6.        System.out.println("Digite o n-ésimo termo da sequência de Fibonacci");
7.        n = sc.nextInt();
8.        start = System.nanoTime();
9.        int result = fib(n);
10.        end = System.nanoTime();
11.        cpu_time_used = (double)(end-start) / 1_000_000_000.00;
12.        System.out.println("O "+n+"º termo de Fibonacci = "+result);
13.        System.out.println("O tempo de execução foi de "+cpu_time_used+" segundos.");
14.}
15.public static int fib(int n) {
16.        if(n==2 || n==1)
17.                return 1;
18.        return fib(n-1) + fib(n-2);
19.}

Dissecação do código

Vamos dissecar esse código em partes para você entendê-lo de maneira mais adequada.

Nas linhas 15-19 tem-se a função/método que calcula o n-ésimo termo da sequência de Fibonacci.

15.public static int fib(int n) {
16.        if(n==2 || n==1)
17.                return 1;
18.        return fib(n-1) + fib(n-2);
19.}

Na linha 8 é obtido o registro de tempo inicial em nano segundos; o tempo antes da execução do algoritmo.

8.start = System.nanoTime();

Na linha 9 é invocada a função fib(), que executa o algoritmo de Fibonacci.

9.int result = fib(n);

Na linha 10 é obtido o registro de tempo final, também em nano segundos; o tempo depois da execução do algoritmo.

10.end = System.nanoTime();

Na linha 11 é calculado o tempo de execução, comparando o antes e o depois.

11.cpu_time_used = (double)(end-start) / 1_000_000_000.00;

Por fim, na linha 13, o tempo de execução é exibido.

13.System.out.println("O tempo de execução foi de "+cpu_time_used+" segundos.");

Resultados

Abaixo são apresentados os tempos de execução (em segundos) para algumas entradas desse algoritmo:

n=40: tempo de execução em torno de 0.4 segundos
n=41: tempo de execução em torno de 0.8 segundos
n=42: tempo de execução em torno de 1.2 segundos
n=43: tempo de execução em torno de 2 segundos
n=44: tempo de execução em torno de 3.1 segundos
n=45: tempo de execução em torno de 5 segundos

Você poderia achar razoável essa forma de medir desempenho. Entretanto, esta é uma péssima ideia.

Estes resultados foram gerados com o algoritmo escrito na linguagem Java, utilizando a IDE Eclipse, em um notebook Intel Core i7. Se estas especificações mudassem, os resultados seriam diferentes, e é aí que reside o problema!

O tempo de execução de um algoritmo, medido em unidades de tempo, pode ser influenciado por diversos fatores, tais como:

• velocidade de processamento do computador;
• linguagens de programação utilizadas;
• compiladores;
• sistema operacional; para citar alguns.

Estes fatores invalidam a confiança dos resultados de desempenho, pois nunca se poderá saber ao certo o tempo de processamento do algoritmo de maneira precisa.

Veja abaixo esse código empírico de medição de tempo em diversas linguagens de programação diferentes.

1.import java.util.Scanner;
2.class Main {
3.        public static void main(String[] args) {
4.                int n;
5.                long start, end;
6.                double cpu_time_used;
7.                Scanner sc = new Scanner(System.in);
8.                System.out.println("Digite o n-ésimo termo da sequência de Fibonacci");
9.                n = sc.nextInt();
10.                start = System.nanoTime();
11.                int result = fib(n);
12.                end = System.nanoTime();
13.                cpu_time_used = (double) (end - start) / 1_000_000_000.00;
14.                System.out.println("O " + n + "º termo de Fibonacci = " + result);
15.                System.out.println("O tempo de execução foi de " + cpu_time_used + " segundos.");
16.        }
17.        public static int fib(int n) {
18.                if (n == 2 || n == 1)
19.                        return 1;
20.                return fib(n - 1) + fib(n - 2);
21.        }
22.}

1.#include <stdio.h>
2.#include <sys/time.h>
3.int fib(int n);
4.int main(void) {
5.        int n;
6.        struct timeval start_d, end_d;
7.        long long start, end;
8.        float cpu_time_used;
9.        printf("Digite o n-ésimo termo da sequência de Fibonacci: ");
10.        scanf("%d", &n);
11.        gettimeofday(&start_d, NULL);
12.        int result = fib(n);
13.        gettimeofday(&end_d, NULL);
14.        start = start_d.tv_sec * 1000LL + start_d.tv_usec / 1000;
15.        end = end_d.tv_sec * 1000LL + end_d.tv_usec / 1000;
16.        cpu_time_used = (end - start) / 1000.0f;
17.        printf("O %dº termo de Fibonacci = %d", n, result);
18.        printf("O tempo de execução foi de %f segundos.", cpu_time_used);
19.}
20.int fib(int n) {
21.        if (n == 2 || n == 1)
22.                return 1;
23.        return fib(n - 1) + fib(n - 2);
24.}

1.#include <stdio.h>
2.#include <sys/time.h>
3.int fib(int n);
4.int main() {
5.        int n;
6.        struct timeval start_d, end_d;
7.        long long start, end;
8.        float cpu_time_used;
9.        std::cout << "Digite o n-ésimo termo da sequência de Fibonacci: ";
10.        std::cin >> n;
11.        gettimeofday(&start_d, NULL);
12.        int result = fib(n);
13.        gettimeofday(&end_d, NULL);
14.        start = start_d.tv_sec * 1000LL + start_d.tv_usec / 1000;
15.        end = end_d.tv_sec * 1000LL + end_d.tv_usec / 1000;
16.        cpu_time_used = (end - start) / 1000.0f;
17.        std::cout << "O " << n << "º termo de Fibonacci = " << result << std::endl;
18.        std::cout << "O tempo de execução foi de " << cpu_time_used << " segundos.";
19.}
20.int fib(int n) {
21.        if (n == 2 || n == 1)
22.                return 1;
23.        return fib(n - 1) + fib(n - 2);
24.}

1.using System;
2.class Program{
3.        public static void Main(string[] args){
4.                int n;
5.                long start, end;
6.                double cpu_time_used;
7.                Console.Write("Digite o n-ésimo termo da sequência de Fibonacci: ");
8.                n = Convert.ToInt32(Console.ReadLine());
9.                start = DateTime.Now.Ticks / TimeSpan.TicksPerMillisecond;
10.                int result = fib(n);
11.                end = DateTime.Now.Ticks / TimeSpan.TicksPerMillisecond;
12.                cpu_time_used = (double)(end - start) / 1000.0;
13.                Console.WriteLine("O " + n + "º termo de Fibonacci = " + result);
14.                Console.WriteLine("O tempo de execução foi de " + cpu_time_used + " segundos.");
15.        }
16.        public static int fib(int n){
17.                if (n == 2 || n == 1)
18.                        return 1;
19.                return fib(n - 1) + fib(n - 2);
20.        }
21.}

1.import time
2.
3.def fib(n):
4.        if (n == 2 or n == 1):
5.                return 1
6.        return fib(n - 1) + fib(n - 2)
7.
8.print("Digite o n-ésimo termo da sequência de Fibonacci: ")
9.n = input()
10.start = round(time.time() * 1000)
11.result = fib(int(n))
12.end = round(time.time() * 1000)
13.cpu_time_used = (end - start) / 1000.0
14.print("O " + str(n) + "º termo de Fibonacci = " + str(result))
15.print("O tempo de execução foi de " + str(cpu_time_used) + " segundos.")

O método analítico para a análise de algoritmos

O método analítico é uma maneira mais assertiva para medir a complexidade de tempo dos algoritmos. Ele não tem o objetivo de calcular o tempo de execução em segundos, minutos ou alguma outra representação real de tempo. Ele visa encontrar uma expressão matemática para traduzir o desempenho em quantidade de instruções. É uma abordagem que busca contabilizar, no próprio algoritmo, a quantidade de instruções que ele executa.

Desta forma, consegue-se medir o desempenho do algoritmo de maneira totalmente independente de linguagens de programação, de compiladores, de ferramentas e de outros fatores físicos que possam invalidar a análise.

Para tanto, o modelo RAM (Random Access Machine) é a estratégia utilizada para medir desempenho de maneira analítica. Ele realiza a contagem das instruções que um algoritmo executa e ignora todos os aspectos de velocidade de processamento, linguagem de programação ou qualquer outro tipo de otimização de hardware.

No modelo RAM, cada operação (tais como, atribuições, comparações e inicializações) consome um custo computacional constante e único. Veja abaixo diversos exemplos de operações computacionais comumente encontrada nos algoritmos, todas com o mesmo custo computacional:

Declaração e atribuição de variáveis

1.int valor = 0; // um único custo computacional
2.float sal = 2005.15; // um único custo computacional

Incremento ou decremento de variáveis

1.valor++; // um único custo computacional
2.valor--; // um único custo computacional

Operações matemáticas complexas

1.valor*(4/Math.sqrt(9)); // um único custo computacional

Acesso a elementos de arrays

1.lista[i]; // um único custo computacional 

Operações lógicas

1.if(valor > 10); // um único custo computacional
2.if(valor==3 || valor==2); // um único custo computacional 

Operações de leitura e escrita

1.System.out.println("Ola mundo!"); // um único custo computacional
2.scanner.nextInt(); // um único custo computacional 

Ou seja, todas as operações computacionais terão um custo computacional único!

É óbvio que, na realidade, estas instruções possuem diferenças significativas de desempenho. Umas são fisicamente mais rápidas de serem executadas do que outras. Contudo, como estamos interessados em analisar o desempenho do algoritmo com base na quantidade de instruções, o modelo RAM ignora tais diferenças. Principalmente pelo fato de que essas diferenças têm mais a ver com os computadores do que com o algoritmo em si.

Análise por contagem de instruções

Para encontrar a complexidade de tempo de um algoritmo por meio do método analítico, basta contar, linha por linha, a quantidade de vezes que cada uma das instruções é executada.

Abaixo segue um código de um programa simples que iremos utilizar como exemplo para começar a explicar a técnica analítica da contagem de instruções.

1.Scanner sc = new Scanner(System.in); // 1 vez
2.int idade; // 1 vez
3.System.out.println("Digite a sua idade:"); // 1 vez
4.idade = sc.nextInt(); // 1 vez
5.if (idade >= 18) // 1 vez
6.        System.out.println("Maior de idade:"); // 1 vez
7.else
8.        System.out.println("Menor de idade:"); // 1 vez 

Após realizada a contagem de instruções do código acima, observamos que o algoritmo realiza um total de 6 instruções (o if-else são mutuamente exclusivos: ou executa o if ou executa o else).

Desta forma, dizemos que T(n)=6 é a fórmula de complexidade de tempo desse algoritmo.

Essa forma de quantificação das instruções proposta pelo modelo RAM permite comparar vários algoritmos uns com os outros e afirmar de maneira mais precisa qual é o mais rápido.

Independente da velocidade dos computadores nos quais são executados, um algoritmo que executa uma menor quantidade de instruções sempre apresentará melhor desempenho para grandes volumes de dados processados.

Definição matemática formal

Uma vez apresentado o modelo RAM e o motivo da sua adoção, pode-se partir para a definição matemática formal da análise da complexidade de tempo de um algoritmo.

Dado um algoritmo ao qual:

• é submetido uma entrada de tamanho n;
• que possui na sua sintaxe um conjunto de instruções Q (condicionais, declaração de variáveis, atribuição, dentre outras);
• onde cada instrução q ∊ Q possui o mesmo custo computacional;
• é denotando por f(q) a quantidade de vezes que cada instrução q é executada no algoritmo (ex.: em uma estrutura de repetição, que pode repetir a mesma instrução q várias vezes),

tem-se que o objetivo da análise da complexidade de tempo, denotada por T(n), é calcular o somatório da quantidade de execução de todas as instruções q do algoritmo para aquela entrada de tamanho n.

Formalmente, representa-se o custo da complexidade de tempo do algoritmo por: ∑q∊Q f(q), ou seja, o somatório do total de execuções de cada uma de suas instruções.

Análise de um comando “for”

Para compreender o método analítico de maneira mais aprofundada, vamos realizar a contagem de instruções em um algoritmo que implementa uma estrutura de repetição (comando for).

Imaginemos, por exemplo, uma função/método bem simples; que recebe uma entrada de tamanho n e determina uma única instrução dentro de um laço de repetição:

1.public static void func(int n){
2.        for(int i=0; i<n; i++){
3.                print(i);
4.        }
5.}

Neste caso, pode-se realizar a contagem de instruções da seguinte maneira:

a inicialização “int i=0” é uma instrução que é executada uma única vez;

2.for(int i=0; i<n; i++){ // 1 vez

a quantidade de incrementos “i++” em um comando for é igual à quantidade de repetições que ele executa, neste caso, n vezes;

2.for(int i=0; i<n; i++){ // n vezes

a quantidade de execução da comparação “i<n” é igual à quantidade de execuções do incremento “i++” mais 1 (esse 1 se refere à comparação que abandona o laço), totalizando n+1 vezes;

2.for(int i=0; i<n; i++){ // n+1 vezes

por fim, dentro do laço, temos uma única instrução que é executada n vezes.

3.print(i); // n vezes

Após contabilizadas as instruções do algoritmo, deve-se fazer o somatório de todas as execuções. Pela definição matemática este algoritmo possui:

• Q = { “int i=0”, “i<n”, “i++”, “print(i)” } // as instruções
• f(“int i=0”) = 1 // quantidade executada pela 1ª instrução
• f(“i<n”) = n+1 // quantidade executada pela 2ª instrução
• f(“i++”) = n // quantidade executada pela 3ª instrução
• f(“print(i)”) = n // quantidade executada pela 4ª instrução
• ∑q∊Q f(q) = 1 + (n+1) + n + n = 3n+2 // custo da complexidade de tempo

Portanto, pode-se dizer que a complexidade de tempo desse algoritmo é T(n) = 1 + n + (n+1) + n, resultando na fórmula T(n)=3n+2.

Desta maneira, pode-se medir com exatidão a quantidade de instruções executadas pelo algoritmo em função da sua entrada de tamanho n, ou seja, o seu desempenho em função da entrada n.

O que fazer com a fórmula de complexidade?

Uma vez encontrada a fórmula de complexidade de um algoritmo, pode-se fazer alguns testes para observar a sua utilidade.

Voltemos ao exemplo da análise do comando for.

1.public static void func(int n){
2.        for(int i=0; i<n; i++){
3.                print(i);
4.        }
5.}

Pudemos observar na seção anterior que esse algoritmo gera uma fórmula de complexidade de tempo T(n)=3n+2.

A partir dessa fórmula, podemos com exatidão descobrir a quantidade de instruções executadas pelo algoritmo para cada uma das entradas n submetidas a ele. Vejamos alguns exemplos:

Caso submetêssemos ao algoritmo o valor n=5, pela fórmula, a quantidade de instruções executadas seria T(5)=3*5+2 ► T(5)=17.

Isso significa que para uma entrada de tamanho 5, o algoritmo executa 17 instruções, ou seja, T(5)=17.

Seguindo o mesmo raciocínio, pode-se calcular que T(10)=32, bem como que T(15)=47.

Análise gráfica da complexidade de um algoritmo

A maior utilidade de uma função de complexidade de tempo é a sua representação gráfica. A representação gráfica permite visualizar o comportamento do algoritmo: a evolução da quantidade de instruções executadas em função do tamanho da entrada n.

Veja o gráfico abaixo que ilustra os resultados para T(5), T(10) e T(15). É possível observar como o desempenho do algoritmo se comporta quando o valor de n tende a crescer.

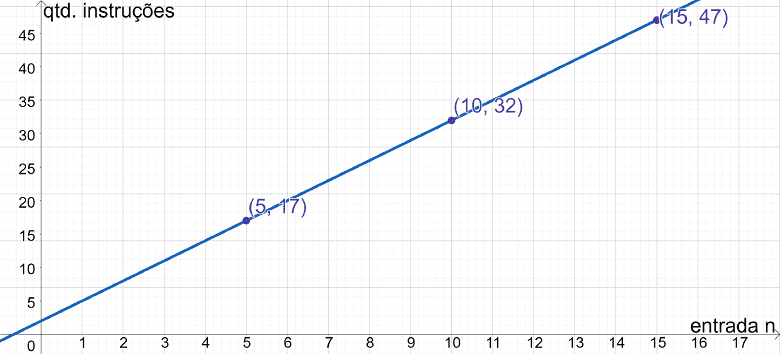
Um gráfico é uma excelente forma de visualizar a fórmula de complexidade T(n) de um algoritmo.

Exercícios

Para demonstrar que você compreendeu bem o técnica de “análise por contagem de instruções” e a “definição matemática formal” da complexidade de tempo de um algoritmo, resolva os exercícios propostos:

Exercício A

Utilizando a técnica da contagem de instruções, encontre a fórmula de complexidade de tempo T(n) para o algoritmo abaixo.

1.public static void func(int n){
2.        for(int i=0; i<n; i++){
3.                print(i);
4.        }
5.        for(int i=0; i<n; i++){
6.                print(i);
7.        }
8.}

Exercício B

Utilizando a técnica da contagem de instruções, encontre a fórmula de complexidade de tempo T(n) para o algoritmo abaixo.

1.public static void func(int n){
2.        for(int i=0; i<n/2; i++){
3.                print(i);
4.        }
5.}

Continue os seus estudos neste curso e leia o próximo artigo sobre “melhor e pior caso” em análise de algoritmos.