Comportamento assintótico

Antes de ler este artigo é necessário que você já tenha lido o artigo sobre melhor caso e pior caso da análise de algoritmos. Se você ainda não leu, clique aqui e confira.

De uma maneira simplificada e mais objetiva possível, o comportamento assintótico pode ser entendido como a curva de crescimento da função gerada pelo processo de análise de algoritmos.

Sabe-se que o objetivo da análise de algoritmos é encontrar uma fórmula fechada (função) T(n) que represente a quantidade de instruções executadas pelo algoritmo em função da sua entrada n.

Por exemplo: o algoritmo findMax() (no pior caso) possui complexidade T(n)=4n. Isso significa que se a sua entrada n for igual a 4 (um array de tamanho 4), a quantidade de instruções executadas pelo algoritmo será igual a:

• T(4) = 4*4 = 16 instruções.

Da mesma forma, se a entrada n for igual a 10 (um array de tamanho 10), a quantidade de instruções executadas pelo algoritmo será igual a:

• T(10) = 4*10 = 40 instruções.

As funções T(n) encontradas pelo processo de análise são de grande importância para mensurar a eficiência dos algoritmos. A ciência da computação usa essas funções T(n) para separar os algoritmos em classes específicas de desempenho. E ela faz isso analisando o seu “comportamento assintótico”.

Para começar a entender o conceito de comportamento assintótico, precisamos analisar a função em um gráfico e observar como a quantidade de instruções cresce em função do valor da entrada n. Para tanto, vamos analisar na próxima seção as funções T(n) de três algoritmos hipotéticos. São eles:

• Algoritmo 1. Complexidade: T(n)=7
• Algoritmo 2. Complexidade: T(n)=3n+2
• Algoritmo 3. Complexidade: T(n)=5n²-n+1

Curva de crescimento das funções

Para cada um dos algoritmos, criaremos um gráfico: (tam. da entrada n) x (qtd. de instruções executadas).

Comportamento assintótico do algoritmo 1: T(n)=7

Este é um algoritmo de complexidade constante. Se olharmos o gráfico da função ilustrado abaixo, percebemos a constância do seu comportamento.

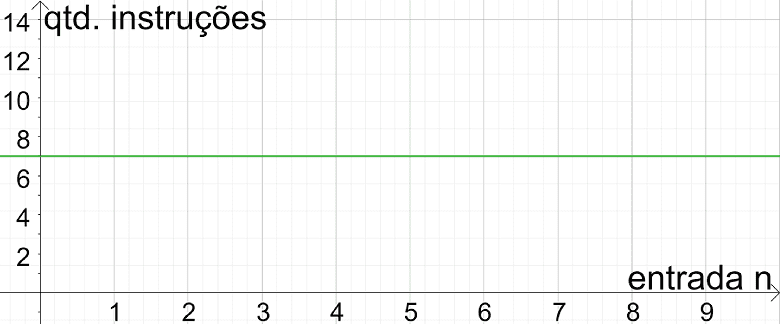
Pode-se observar no gráfico acima que a quantidade de instruções executadas (eixo vertical) não cresce em função dos valores de n (eixo horizontal). O número de instruções sempre permanece igual a 7.

Comportamento assintótico do algoritmo 2: T(n)=3n+2

Este é um algoritmo de complexidade linear. Se olharmos o gráfico da função ilustrado abaixo, percebemos que o número de instruções executadas pelo algoritmo (eixo vertical) cresce de maneira linear, em relação aos valores de n (eixo horizontal).

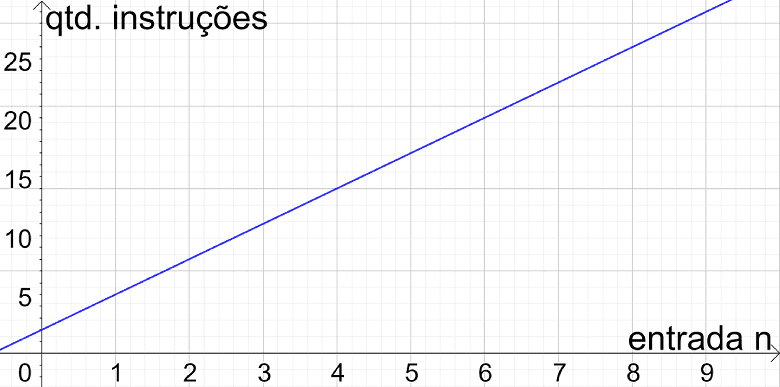
Comportamento assintótico do algoritmo 3: T(n)=5n²-n+1

O algoritmo 3 possui complexidade quadrática. Se olharmos o gráfico da função ilustrado abaixo, percebemos que o número de instruções executadas pelo algoritmo (eixo vertical) cresce de maneira quadrática em relação aos valores de n (eixo horizontal).

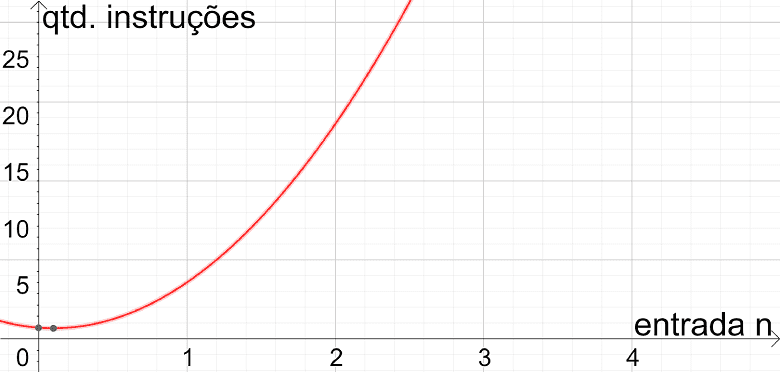
Comparação entre os algoritmos

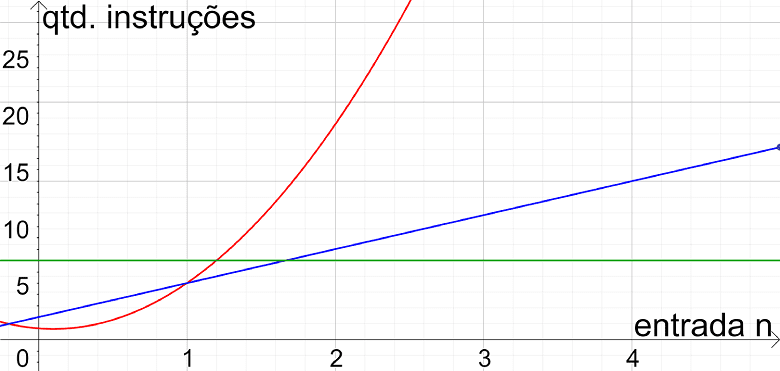
Quando sobrepomos os gráficos das funções de complexidade dos três algoritmos (imagem abaixo), podemos perceber a tendência de crescimento de cada uma das funções. Observe como a função quadrática tende a apresentar uma quantidade de instruções cada vez maior para cada novo tamanho n da entrada! Isso significa que o algoritmo quadrático é menos eficiente que os outros dois, os quais possuem uma tendência de crescimento menor.

Um comportamento assintótico equivocado

Vamos a um exemplo bem ilustrativo para mostrar a importância do comportamento assintótico dos algoritmos. Foi realizada uma análise em dois algoritmos (A e B) que resultou nas seguintes funções de complexidade:

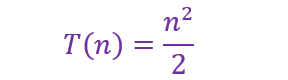
Algoritmo A

Algoritmo B

Pergunta: Qual o algoritmo mais eficiente?

Observe abaixo uma tabela que mostra a quantidade de instruções executadas, por cada um deles, para os valores iniciais de n:

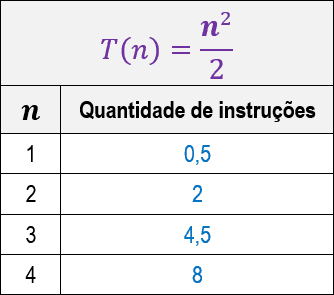
Aparentemente (olhando a tabela) somos tentados a dizer que o algoritmo A é mais eficiente por apresentar quantidades de instruções bem menores para os mesmos valores de n.

Mas observe abaixo o que acontece quando analisamos a quantidade de instruções para valores maiores de n:

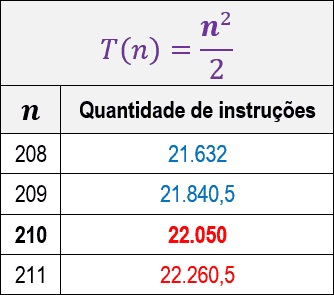
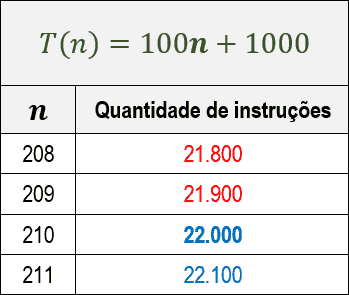
Observe que até o valor de n=209 o algoritmo A é mais eficiente que o B, mas a partir do valor de n=210 o quadro se inverte e o algoritmo B passa a ser mais eficiente que o A.

As constantes multiplicativa e aditiva, respectivamente 100 e 1000 (na função do algoritmo B), dão a falsa impressão de que ele é menos eficiente, mas elas só adiam o inevitável.

Veja abaixo o gráfico plotado para ambas as funções. Perceba como, a partir do valor de n=210, a quantidade de instruções executadas pelo algoritmo B é superada pela do algoritmo A:

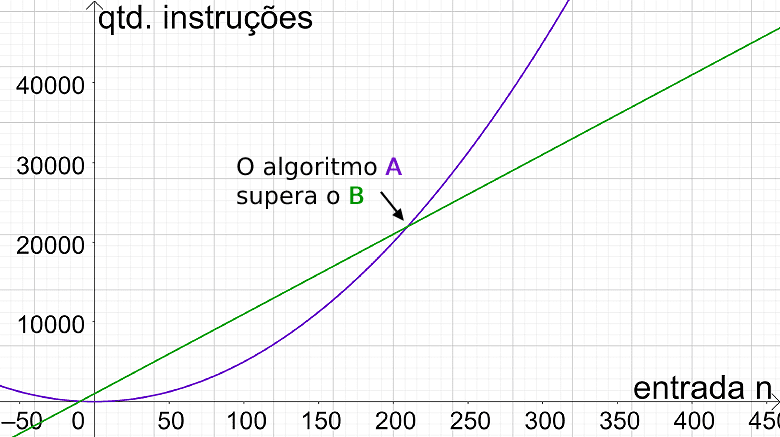
O que acabamos de fazer neste exemplo foi analisar o comportamento assintótico dos dois algoritmos. Analisamos a tendência de crescimento das instruções dos algoritmos quando n possui um valor muito grande, quando n tende ao infinito (n → ∞).

O fato do algoritmo A ser quadrático já nos dá a pista de que, para valores muito grandes de n (n → ∞), a sua quantidade de instruções irá superar a quantidade de instruções do algoritmo B, que por sua vez é linear. Por este motivo, todas as constantes aditivas e multiplicativas da função de complexidade de um algoritmo não exercem nenhum impacto no seu comportamento assintótico (a sua tendência de crescimento no gráfico).

Desta forma, entende-se que: nem o denominador 2 (do algoritmo A) e nem o fator 100 e a parcela 1000 (do algoritmo B) podem impedir que o algoritmo B seja mais eficiente que o A para grandes valores de n.

Exercício

Para que você possa praticar o conceito de comportamento assintótico de funções, tente resolver o exercício proposto.

• Algoritmo A: T(n) = n(n+5)
• Algoritmo B: T(n) = 10n+10

Analise graficamente as funções T(n) de complexidade de tempo dos algoritmos A e B acima e determine:

1. Qual é o algoritmo “mais eficiente” e o “menos eficiente”?
2. Em qual valor de n o “menos eficiente” supera o “mais eficiente”?

Prossiga com os estudos neste curso e leia o próximo artigo sobre classes assintóticas” em análise de algoritmos.