Big Omega notation

In the last article we met the first notation used in computer science to define asymptotic behavior of algorithms: the Big O notation. In this article we will teach you the second computational notation used for the analysis of algorithms: the Big Omega notation, represented by the Greek letter Ω.

If you haven’t read the article about the Big O notation, click on this link and access the article where we explain in detail about this. It is highly recommended that you have some knowledge of Big O notation before reading this article!

In the most straightforward way possible, the Ω notation provides us with a simplified symbology to represent a lower performance bound for an algorithm. A minimum threshold of time that an algorithm takes to run. That is, the Ω notation is the inverse of the Big O notation.

Let’s look at some practical examples to help you begin to understand the meaning and use of the Ω notation.

Example for linear function

When we say that the 4n-3 function is Ω(n) (read “is omega of n”), we are saying that the asymptotic behavior of a linear function is equal to or less than its own. That is to say: the 4n-3 function will never have a growth behavior inferior to that of a function with linear behavior.

In this way, Ω(n) presents itself as a lower limit, and we know that the 4n-3 function will never show a growth behavior that is exceeded by this lower limit.

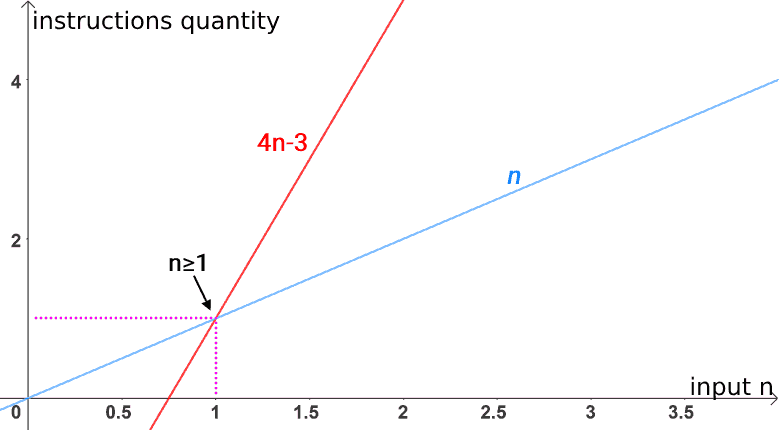
Example: for the function 4n-3, there is another function with linear behavior that limits it below. Notice in the graph below that, for values of n≥1, the 4n-3 function outperforms the n function.

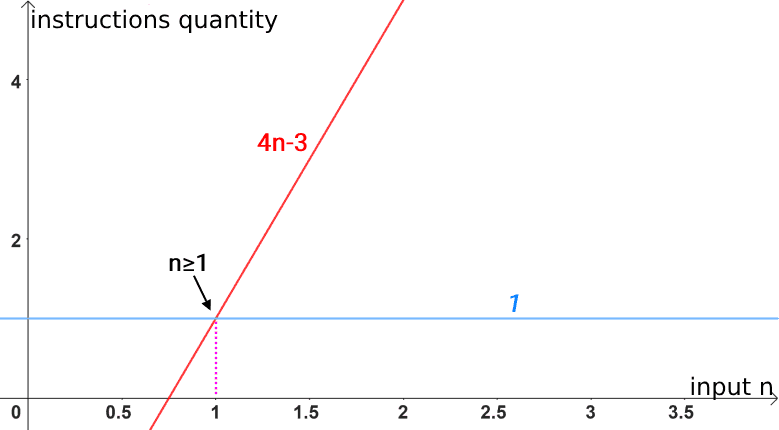
Likewise, it is also correct to state that 4n-3 is Ω(1), as the function 4n-3 will never show a growth behavior that is surpassed by a constant behavior. Thus, Ω(1) also presents itself as a lower asymptotic limit:

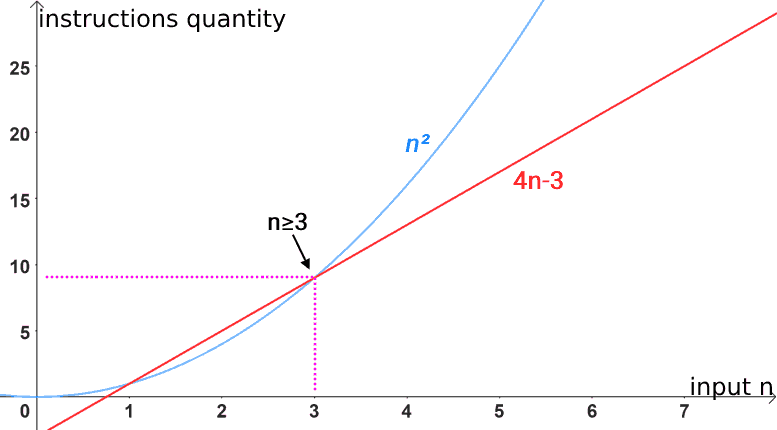
Now, it would be wrong to say that 4n-3 is Ω(n²), as the function 4n-3 will never grow to the point of overcoming quadratic behavior. In this way, Ω(n²) is not presented as an lower asymptotic limit:

In short:

4n-3 is not Ω(n²), because it cannot overcome (can’t limit below) a quadratic function.

4n-3 is Ω(n), because it can overcome (can limit below) a linear function.

4n-3 is Ω(1), because it can overcome (can limit below) a linear function.

Example for quadratic function

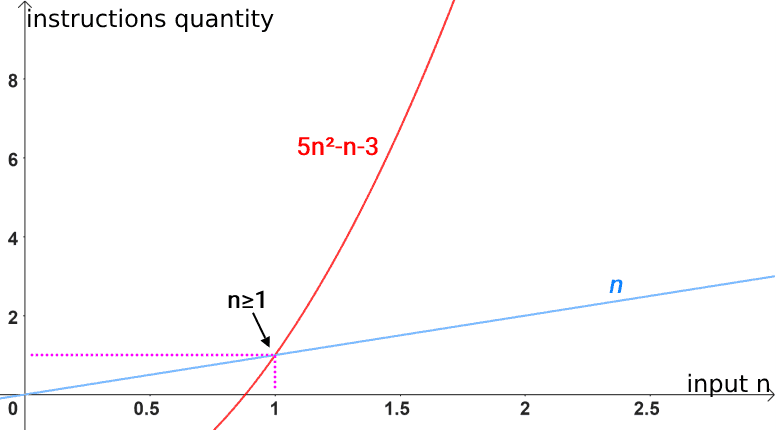
When we say that the function 5n²-n-3 is Ω(n²), we are saying that: “the asymptotic behavior of a quadratic function is equal to or less than its”. That is to say: the 5n²-n-3 function will never have a growth behavior lower than that of a function with quadratic behavior.

In this way, Ω(n²) is presented as a lower limit, and we know that the function 5n²-n-3 will never show a growth behavior that is exceeded by this lower limit.

Notice in the graph below that: for the function 5n²-n-3, there is another function (n²) with quadratic behavior that limits it from below. Note that, for values of n≥1, the 5n²-n-3 function outperforms the n² function.

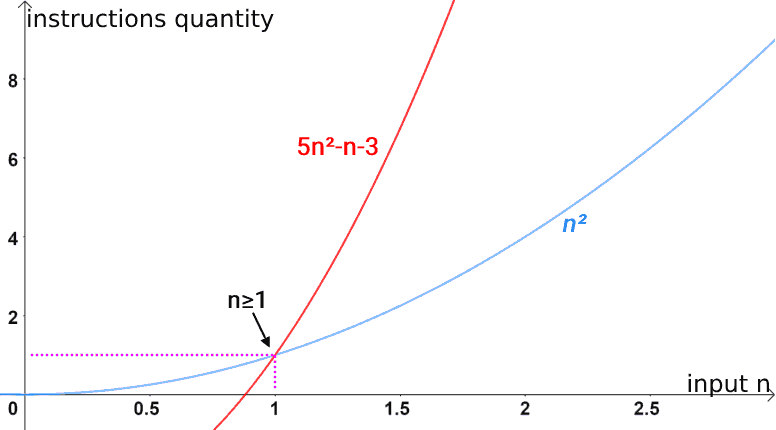
Likewise, it is also correct to state that the quadratic function 5n²-n-3 is Ω(n), as the function 5n²-n-3 will never show a growth behavior that is surpassed by a linear behavior. Therefore, Ω(n) also presents itself as an lower asymptotic limit:

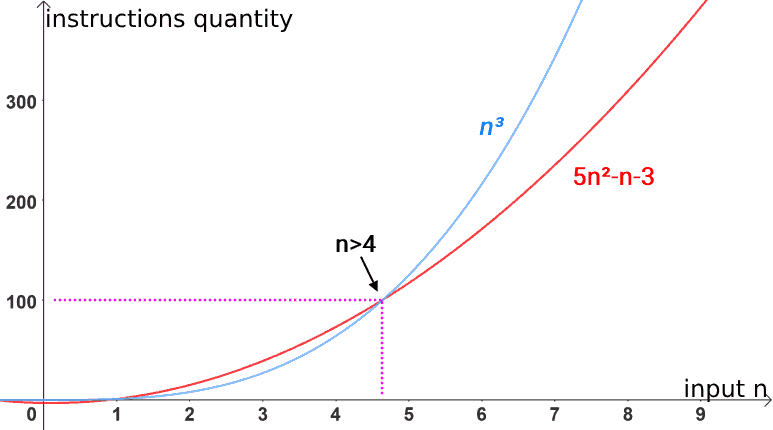
On the other hand, it would be wrong to say that the 5n²-n-3 function is Ω(n³), as the 5n²-n-3 function will never grow to the point of surpassing cubic behavior. In this way, Ω(n³) is not presented as an lower asymptotic limit:

In short:

5n²-n-3 not is Ω(n³), because it cannot overcome (can’t limit below) a cubic function.

5n²-n-3 is Ω(n²), because it can overcome (can limit below) a quadratic function.

5n²-n-3 is Ω(n), because it can overcome (can limit below) a quadratic function.

Formal mathematical definition

Given two algorithm time complexity functions: f(n) and g(n). The formal mathematical definition states that:

• f(n) = Ω(g(n)) (read “f of n is Omega of g of n”) if there are positive constants c and n₀, such that f(n) ≥ c.g(n) for all n ≥ n₀.

This definition seems a little complicated to understand at first sight, but we will demonstrate it with some practical examples.

Mathematical resolution: 1st example

Let’s try to demonstrate by definition that 4n+1=Ω(n) (read as “is Omega of n”).

First, we have to:

• f(n) = 4n+1
• g(n) = n

If, by mathematical definition, we need to demonstrate that there is a positive constant c and a positive n₀ initial value, so that:

• f(n) ≥ c.g(n) for all n ≥ n₀

So, for this problem, we need to show that:

• 4n+1 ≥ c.n for all n ≥ n₀

In summary: we need to prove that, for all values of n greater than or equal to n₀, the function 4n+1 is greater than or equal to c multiplied by n.

To do so, the first decision we need to make is to choose a value for the constant c. In this case, let’s consider c equal to the value 4. See below a table that shows the inequality results for c=4 and for some values of n:

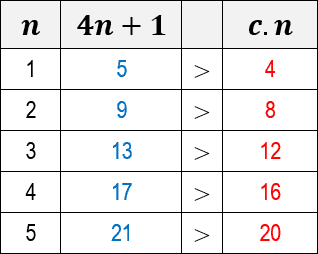
Note that, for all n values expressed in the table, the function of the 4n+1 algorithm is always one unit greater than c.n. When we plot a graph for both functions, we can see more clearly how the 4n+1 function grows more than the c.n function:

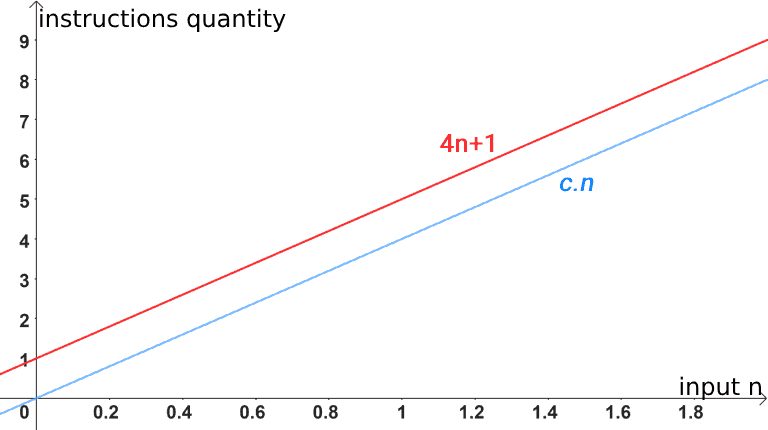
This means that Ω(n) represents an lower asymptotic limit for the function 4n+1, that is, there is a constant c=4 and n₀=1, such that 4n+1 ≥ c.n for all values of n greater than or equal to n₀.

In this way, it is proved that, in fact, 4n+1 = Ω(n).

Mathematical resolution: 2nd example

Let’s try to demonstrate by definition that 5n²-n-3=Ω(n²) (read “is Omega of n squared”).

First, we have to:

• f(n) = 5n²-n-3
• g(n) = n²

If, by mathematical definition, we need to demonstrate that there is a positive constant c and a positive n₀ initial value, so that:

• f(n) ≥ c.g(n) for all n ≥ n₀

So, for this problem, we need to show that:

• 5n²-n-3 ≥ c.n² for all n ≥ n₀

In short: we need to prove that, for all values of n greater than or equal to n₀, the function 5n²-n-3 is greater than or equal to c multiplied by n².

Again, we need to choose a value for the c constant. In this case, we will also consider c equal to the value 4. See below a table that shows the inequality results for c=4 and for some values of n:

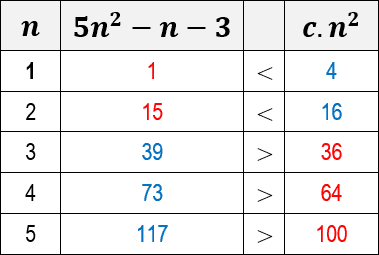
Note that, for all values of n>2 expressed in the table, the function of the algorithm 5n²-n-3 is each time greater than c.n². When we plot a graph for both functions, we can see more clearly how the 5n²-n-3 function grows more than the c.n² function.

This means that Ω(n²) represents an lower asymptotic limit for the function 5n²-n-3, that is, there is a constant c=4 and n₀=3, such that 5n²-n-3 ≥ c.n² for all values of n greater than or equal to n₀.

In this way, it is proved that, in fact, 5n²-n-3 = Ω(n²).

Mathematical resolution: 3rd example (wrong)

Let’s try to demonstrate by definition that 2n+1=Ω(n²).

First, we have to:

• f(n) = 2n+1
• g(n) = n²

If, by mathematical definition, we need to demonstrate that there is a positive constant c and a positive n₀ initial value, so that:

• f(n) ≥ c.g(n) for all n ≥ n₀

So, for this problem, we need to show that:

• 2n+1 ≥ c.n² for all n ≥ n₀

In short: we need to prove that, for all values of n greater than or equal to n₀, the function 2n+1 is greater than or equal to c multiplied by n².

At first glance, it can be seen that 2n+1 has linear behavior and c.n² has quadratic behavior. Thus, it is clear that this proof is false, as a quadratic function (c.n²) cannot represent an lower asymptotic limit for a linear function (2n+1).

However, we will carry out a more in-depth analysis to understand the reason for this impossibility.

Let’s carry out some algebraic transformations in order to isolate the constant c in the inequality and understand its possible values:

The resulting inequality already shows us the impossibility of existing any constant c that makes it valid for large values of n (n→∞), because, regardless of how large the value of c is, the denominator n² will always make the result of the function ever smaller.

Note in the table below how the value of the function gets smaller and smaller when compared to the value of c (considering c=1, which is its minimum value). It can be seen that the values of the function approach zero as the value of n increases.

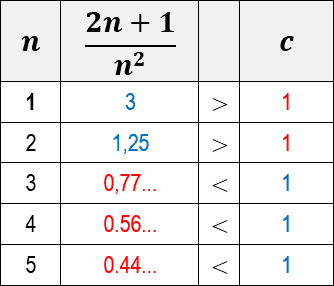
This means that, even with the smallest possible value for the constant c, the function will always decrease to the point of becoming smaller than the constant.

Therefore, we were unable to demonstrate our objective. There is no constant c and n₀, such that 2n+1 ≥ c.n² for all values of n greater than or equal to n₀.

In this way, it is proved that, in fact, 2n+1≠Ω(n²)(read as “it is not Omega of n squared”).

Exercises

To demonstrate that you have a good understanding of the concept and the formal mathematical definition of Big Omega notation, solve the proposed exercises:

Exercises A

Try to prove mathematically that n²+800 = Ω(n).

Try to prove mathematically that 2n+10 = Ω(n).

Try to prove mathematically that n+10 = Ω(n²).

Try to prove mathematically that 7n-2 = Ω(1).

Try to prove mathematically that n²+20n+5 = Ω(n³).

Exercise B

Using the instruction counting technique, find the complexity formula T(n) of the algorithm below and then try to mathematically demonstrate that this formula found is Ω(n²).

1.public static void func(int[ ] n){
2.    for (int i=0; i<n.length-1; i++) {
3.        n[i]=i+i;
4.    }
5.}

Continue your studies in this course and read the next article about the last of three notations used in computing to represent the asymptotic behavior of algorithms: “Theta notation”.