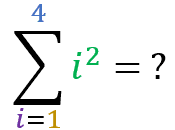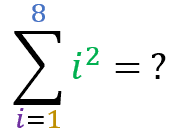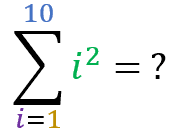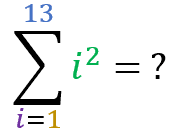The properties of the summation allow us to perform powerful algebraic simplifications on equations involving this type of mathematical symbology. This article divides the properties of the summation into two categories:
- first we present the properties of the summation applied to the elements of numeric sets.
- then, the properties applied to the polynomial functions are presented.
If you do not know what a summation is yet, we strongly recommend that before proceeding click on this link and read the article where we explain in detail about it.
Summation properties in numeric set elements
There are some interesting properties of summation for numeric set. These properties are very useful and allow us to save time and effort in solving various types of problems. Let’s go to the properties.
Scalar product:
Let X be a set of real values and α any scalar (value used to multiply). The property states that:
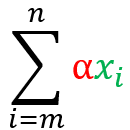
The summation of the scalar multiplied by the term.
=
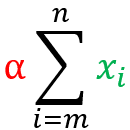
is equal to scalar multiplied by the summation of the term.
Let’s go to the demo:
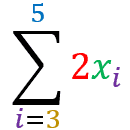
=
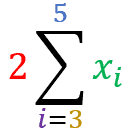
A little exercise for you to practice:
for set Y = { 51 , 72 , 93 , 44 , 105 } show that:
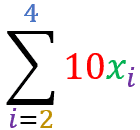
=
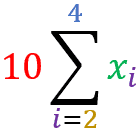
Addition and Subtraction:
Let X and Y be two distinct sets of real values. The property states that:
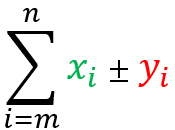
The summation of term X ± term Y
=
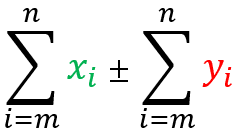
is equal the summation of the term X ± the sum of the term Y
Let’s go to the demo (first with the addition):
Set X = { 101 , 32 , 53 , 74 , 25 , 96 , 47 } and Set Y = { 51 , 62 , 13 , 44 , 85 , 36 , 107 }
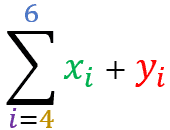
=
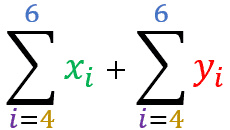
Now let’s go to the demo with the subtraction:
Set X = { 101 , 32 , 53 , 74 , 25 , 96 , 47 } and Set Y = { 51 , 62 , 13 , 44 , 85 , 36 , 107 }
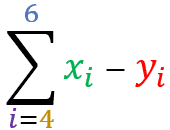
=
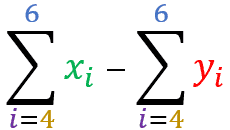
A little exercise for you to practice:
For sets X = { 51 , 72 , 93 , 44 , 105 } and Y = { 21 , 52 , 13 , 44 , 75 } demonstrate that:
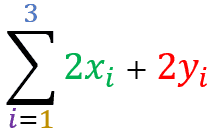
=
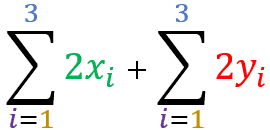
Sum of one step:
Let X be a set of real values. The property states that:
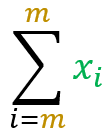
=
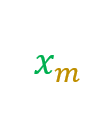
Set X = { 101 , 32 , 53 , 74 , 25 , 96 , 47 }
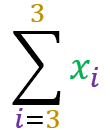
=
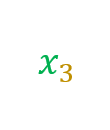
x3
it’s the same as
x3
5
it’s the same as
5
Summation properties in polynomial functions
With respect to polynomial functions, the summation can be converted into ready-made formulas. This can greatly help in performing various algebraic operations.
Summation of 1:
The property states that:
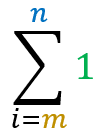
=
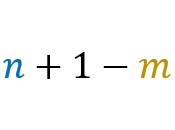
Let’s go to the demo:
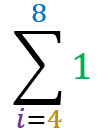
=
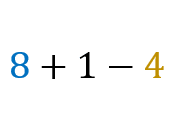
14 + 15 + 16 + 17 + 18
it’s the same as
9 – 4
5
it’s the same as
5
Now let’s test your learning. Using the “summation of 1” formula, calculate the results of the following sums:
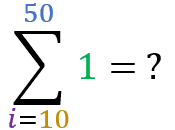
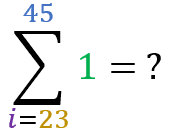
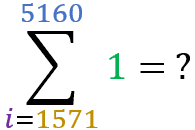
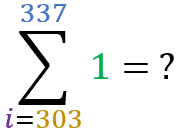
Summation of an arithmetic progression:
The property states that:
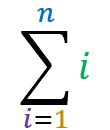
The summation where the term is the sum index itself, in a range from 1 to n, is equal to
=
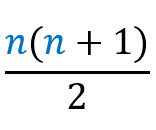
Let’s go to the demo:
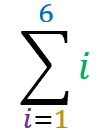
=
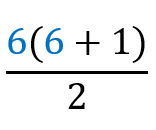
1+2+3+4+5+6
it’s the same as
(6.7)/2
21
it’s the same as
21
Now let’s test your learning. . Using the “summation of a progression” formula, calculate the result of the following sums:
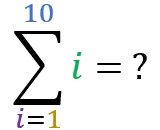
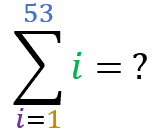
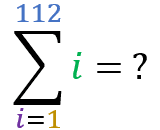
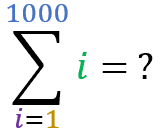
Square Pyramidal Number:
The property states that:
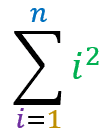
The sum where the term is the squared sum index itself, in a range from 1 to n, is equal to
=
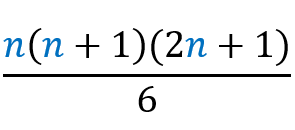
Let’s go to the demo:
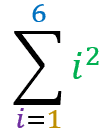
=
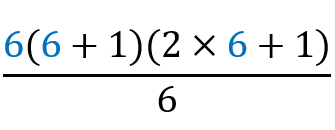
12+22+32+42+52+62
it’s the same as
(42.13)/6
1+4+9+16+25+36
it’s the same as
546/6
91
it’s the same as
91
Now let’s test your learning. Using the “square pyramidal number” formula, calculate the results of the following summation: