Summation is a mathematical symbology used to represent successive sums of terms in a sequence. It is commonly used to represent formulas and expressions involving successive sums of elements, such as the arithmetic mean and formulas used in the area of statistics.
By the end of this article, we will give you not only the definition of summation, but also several examples that show in practice how your representation works.
Definition
This mathematical notation uses the Greek letter ∑ (Sigma) and allows to reduce the size of the representation of a long sum to a single expression. See the example below:
3+4+5+6+7+8+9+10+11+12+13+14
A looooong sum expression
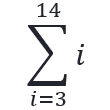
Can be represented as a summation
Just see how, by definition, the concept of summations is quite simple.
Now let’s understand the elements that make up the body of summation symbology. It is made up of some point elements.
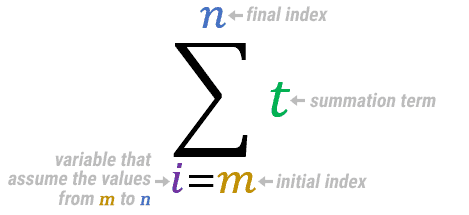
At the top we have the symbol n, which represents the final index of the sum (up to which value the sum will be performed).
At the bottom is the symbol m, which represents the initial index of the sum (from which value the sum will be started).
The i represents the variable that will assume all values between m and n, starting with m. e.g.
For a summation whose values m and n are 2 and 5 respectively
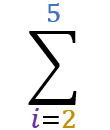
The symbol i represent the values 2,3,4,5 in each step of the summation.
The symbol t represents the summation term. Represents what will be added during the steps. The meaning of this term depends on the formula and the use of the summation. Here are some miscellaneous examples to understand how the summation term can be used.
Situation where the term is the summation index itself:
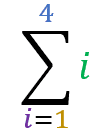
1+2+3+4 = 10
Note in this situation that each step in the summation is nothing more than the index itself in that step.
The following example illustrates a situation where the term is a constant value:
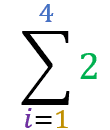
2+2+2+2 = 8
Notice in this situation that each step of the sum is nothing but the value 2. There are four steps (from 1 a 4) adding the only value 2.
The next example shows a more sophisticated (and even more useful) use of summations. The summation term is a function:
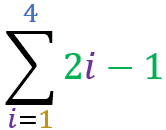
(2x1-1)+( 2x2-1)+( 2x3-1)+( 2x4-1) = 1+3+5+7 = 16
Note that each step of the sum uses the value of i and replaces it in function 2i – 1.
Now that you have got the hang of it, try to find the result for the following summations:
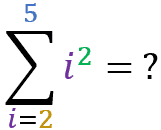
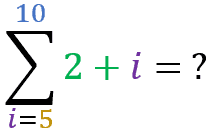
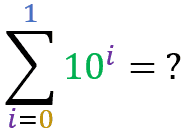
Summation of set elements
Summation symbol is also used to perform sum of terms in a set. Note the following example:
Imagine a set of seven values X = { 101 , 32 , 53 , 74 , 25 , 96 , 47 }, where the value 10 is the element in position 1, the 3 is the element in position 2, onwards… Up to the element 4 at position 7. We can use summation notation to represent sums of elements of this set. See the example:
for set X = { 101 , 32 , 53 , 74 , 25 , 96 , 47 }
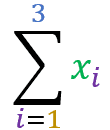
x 1+x 2+x 3 = 10+3+5 = 18
This summation indicates that the first 3 terms of set X will be summed. The term x i indicates that, at each step, the elements of set X will be summed at positions i.
Here’s another example:
for set X = { 101 , 32 , 53 , 74 , 25 , 96 , 47 }
x3+x4+x5+x6+x7 = 5+7+2+9+4 = 27
This summation indicates that the elements of positions 3, 4, 5, 6 and 7 of set X will be summed.
for set Y = { 1001 , 302 , 203 , 254 , 25 }
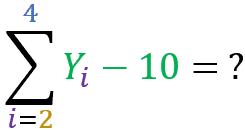
See how easy it is to understand the summations concept! Incidentally, any subject becomes easy to learn when it is explained the right way.
Understanding the summation is just the first step. Understanding the summation is just the first step. What you really need to know is how to use the properties of the summations, because it will allow you to solve more complex equations and problems.
Click here to access the article where we explain in detail about the properties of the summations.
