Notação Big Ômega

No último artigo conhecemos a primeira notação utilizada na ciência da computação para definir comportamento assintótico de algoritmos: a notação Big O. Neste artigo te ensinaremos a segunda notação computacional utilizada para a análise de algoritmos: a notação Big Ômega (ou apenas Ômega), representada pela letra grega Ω.

Se você ainda não leu o artigo sobre a notação Big O, clique neste link e acesse o artigo onde explicamos detalhadamente sobre o assunto. É altamente recomendado que você tenha algum conhecimento sobre a notação Big O antes de ler este artigo!

Da maneira mais objetiva possível, a notação Ω nos fornece uma simbologia simplificada para representar um limite inferior de desempenho para um algoritmo. Um limite mínimo de tempo que um algoritmo leva para ser executado. Ou seja, a notação Ω é o inverso da notação Big O.

Vamos a alguns exemplos práticos para você começar a compreender o significado e o uso da notação Ω.

Exemplo para função linear

Quando dizemos que a função 4n-3 é Ω(n) (lê-se “é ômega de n”), estamos afirmando que o comportamento assintótico de uma função linear é igual ou inferior ao dela. Significa dizer: a função 4n-3 nunca terá um comportamento de crescimento inferior ao de uma função com o comportamento linear.

Desta forma, Ω(n) apresenta-se como um limite inferior, e sabemos que a função 4n-3 nunca apresentará um comportamento de crescimento que seja ultrapassado por esse limite inferior.

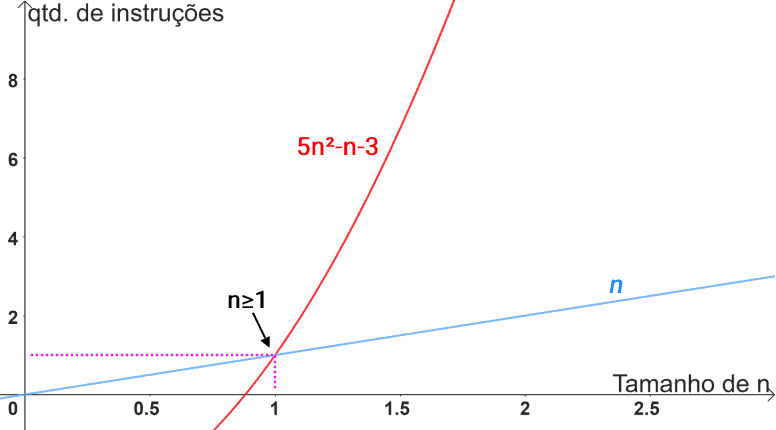
Exemplo: para a função 4n-3, existe uma outra função de comportamento linear que a limita inferiormente. Perceba no gráfico abaixo que, para valores de n≥1, a função 4n-3 supera a função n.

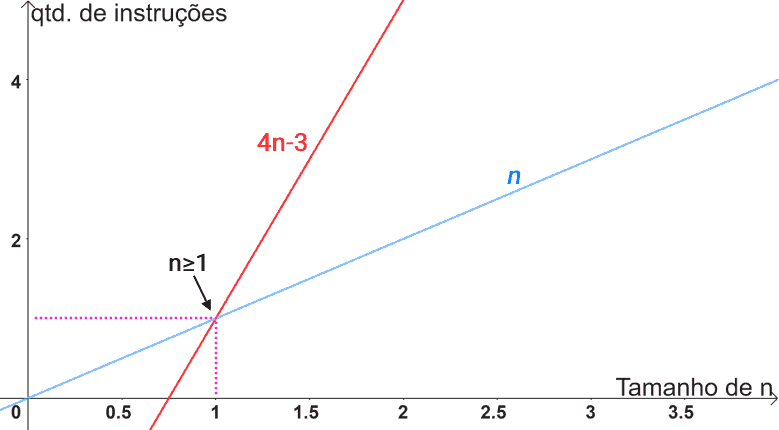
Da mesma forma, também é correto afirmar que 4n-3 é Ω(1), pois a função 4n-3 nunca apresentará um comportamento de crescimento que seja ultrapassado por um comportamento constante. Desta forma, Ω(1) também se apresenta como um limite assintótico inferior:

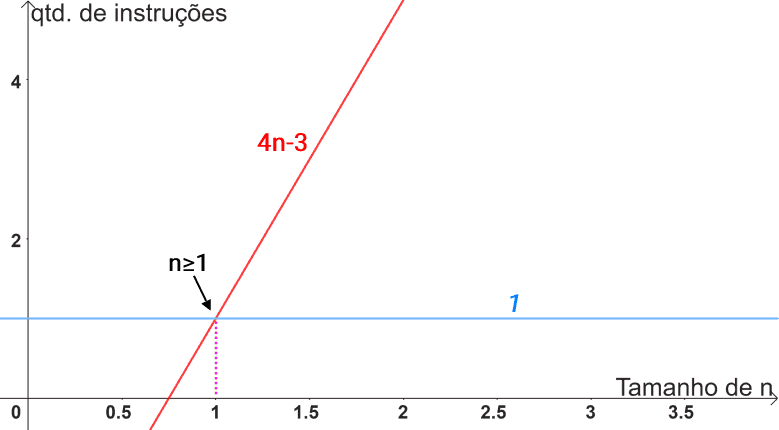
Agora, seria errado dizer que 4n-3 é Ω(n²), pois a função 4n-3 nunca crescerá a ponto de ultrapassar o comportamento quadrático. Desta forma, Ω(n²) não se apresenta como um limite assintótico inferior:

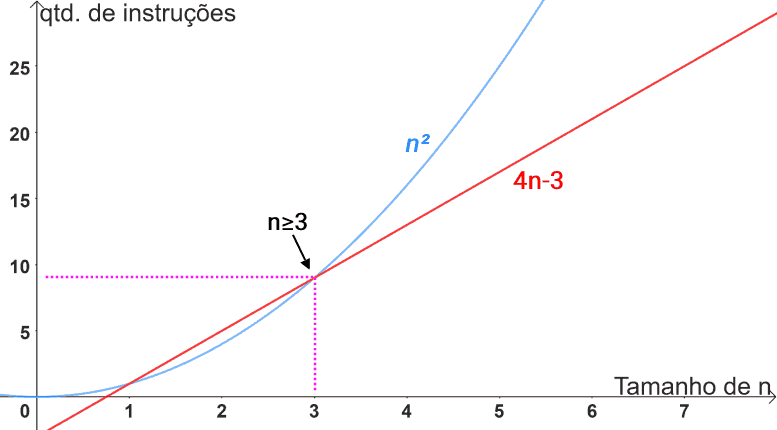
Resumindo:

4n-3 não é Ω(n²), pois não pode superar (limitar inferiormente) uma função quadrática.

4n-3 é Ω(n), pois pode superar (limitar inferiormente) uma função linear.

4n-3 é Ω(1), pois pode superar (limitar inferiormente) uma função constante.

Exemplo para função quadrática

Quando dizemos que a função 5n²-n-3 é Ω(n²), estamos afirmando que: “o comportamento assintótico de uma função quadrática é igual ou inferior ao dela”. Significa dizer: a função 5n²-n-3 nunca terá um comportamento de crescimento inferior ao de uma função com o comportamento quadrático.

Desta forma, Ω(n²) apresenta-se como um limite inferior, e sabemos que a função 5n²-n-3 nunca apresentará um comportamento de crescimento que seja ultrapassado por esse limite inferior.

Perceba no gráfico abaixo que: para a função 5n²-n-3, existe uma outra função (n²) de comportamento quadrático que a limita inferiormente. Perceba que, para valores de n≥1, a função 5n²-n-3 supera a função n².

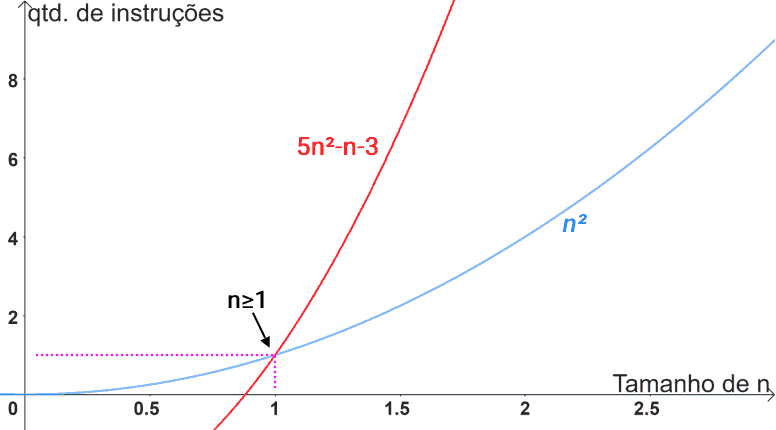
Da mesma forma, também é correto afirmar que a função quadrática 5n²-n-3 é Ω(n), pois a função 5n²-n-3 nunca apresentará um comportamento de crescimento que seja ultrapassado por um comportamento linear. Portanto, Ω(n) também se apresenta como um limite assintótico inferior:

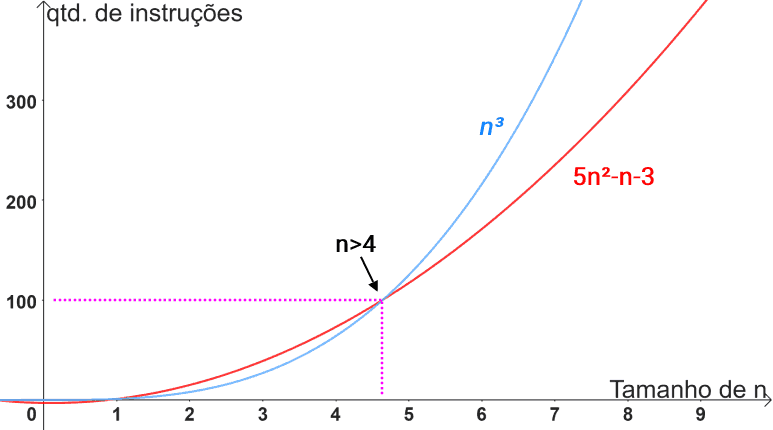
Por outro lado, seria errado dizer que a função 5n²-n-3 é Ω(n³), pois a função 5n²-n-3 nunca crescerá a ponto de ultrapassar o comportamento cúbico. Desta forma, Ω(n³) não se apresenta como um limite assintótico inferior:

Resumindo:

5n²-n-3 não é Ω(n³), pois não pode superar (limitar inferiormente) uma função cúbica.

5n²-n-3 é Ω(n²), pois pode superar (limitar inferiormente) uma função quadrática.

5n²-n-3 é Ω(n), pois pode superar (limitar inferiormente) uma função linear.

Definição matemática formal

Dada duas funções de complexidade de tempo de algoritmos: f(n) e g(n). A definição matemática formal estabelece que:

• f(n) = Ω(g(n)) (lê-se “f de n é Ômega de g de n”) se existirem constantes positivas c e n₀, tais que f(n) ≥ c.g(n) para todos os n ≥ n₀.

Essa definição parece um pouco complicada de se compreender à primeira vista, mas vamos demonstrar com alguns exemplos práticos.

Resolução matemática: 1º exemplo

Vamos tentar demonstrar pela definição que 4n+1=Ω(n) (lê-se “é Ômega de n”).

Primeiramente, temos que:

• f(n) = 4n+1
• g(n) = n

Se, pela definição matemática, precisamos demonstrar que existe uma constante positiva c e um valor positivo n₀ inicial, de forma que:

• f(n) ≥ c.g(n) para todos os n ≥ n₀

Então, para este problema, precisamos mostrar que:

• 4n+1 ≥ c.n para todos os n ≥ n₀

Em resumo: precisamos provar que, para todos os valores de n maiores ou igual a n₀, a função 4n+1 é maior ou igual a c multiplicado por n.

Para tanto, a primeira decisão que precisamos tomar é escolher um valor para a constante c. Neste caso, vamos considerar c igual ao valor 4. Observe abaixo uma tabela que mostra os resultados da desigualdade para c=4 e para alguns valores de n:

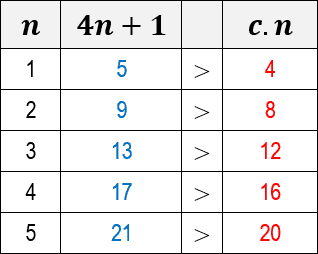
Observe que, para todos os valores de n expressos na tabela, a função do algoritmo 4n+1 é sempre uma unidade maior que c.n. Quando plotamos um gráfico para ambas as funções, visualizamos com maior clareza como a função 4n+1 cresce mais que a função c.n:

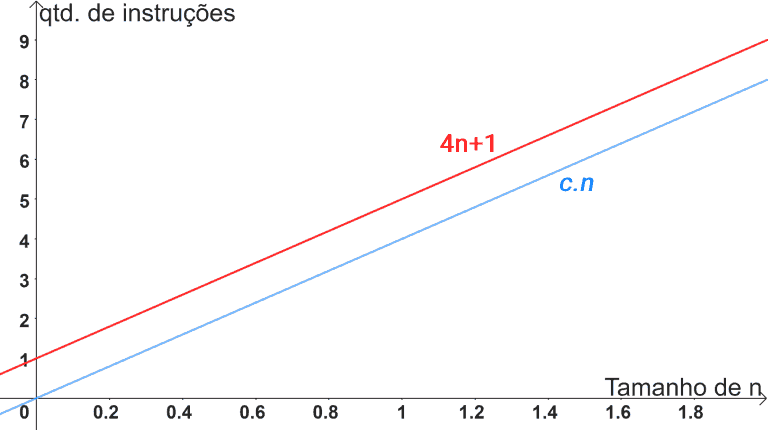
Isso significa que Ω(n) representa um limite assintótico inferior para a função 4n+1, ou seja, existe uma constante c=4 e um n₀=1, tal que 4n+1 ≥ c.n para todos os valores de n maiores ou igual a n₀.

Desta forma, está provado que, de fato, 4n+1 = Ω(n).

Resolução matemática: 2º exemplo

Vamos tentar demonstrar pela definição que 5n²-n-3=Ω(n²) (lê-se “é Ômega de n ao quadrado”).

Primeiramente, temos que:

• f(n) = 5n²-n-3
• g(n) = n²

Se, pela definição matemática, precisamos demonstrar que existe uma constante positiva c e um valor positivo n₀ inicial, de forma que:

• f(n) ≥ c.g(n) para todos os n ≥ n₀

Então, para este problema, precisamos mostrar que:

• 5n²-n-3 ≥ c.n² para todos os n ≥ n₀

Em suma: precisamos provar que, para todos os valores de n maiores ou igual a n₀, a função 5n²-n-3 é maior ou igual a c multiplicado por n².

Novamente, precisamos escolher um valor para a constante c. Neste caso, também vamos considerar c igual ao valor 4. Observe abaixo uma tabela que mostra os resultados da desigualdade para c=4 e para alguns valores de n:

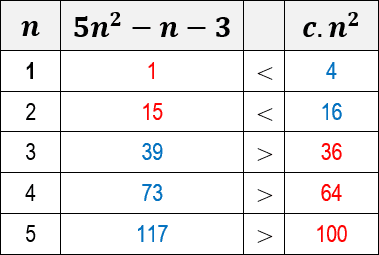
Observe que, para todos os valores de n>2 expressos na tabela, a função do algoritmo 5n²-n-3 é cada vez maior que c.n². Quando plotamos um gráfico para ambas as funções, visualizamos com maior clareza como a função 5n²-n-3 cresce mais que a função c.n².

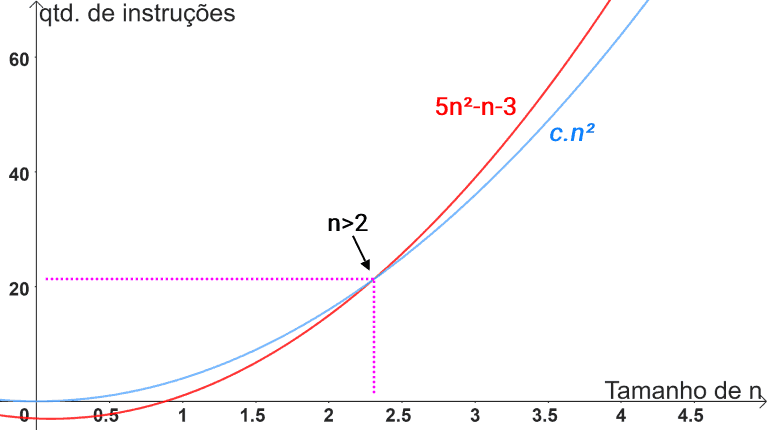
Isso significa que Ω(n²) representa um limite assintótico inferior para a função 5n²-n-3, ou seja, existe uma constante c=4 e um n₀=3, tal que 5n²-n-3 ≥ c.n² para todos os valores de n maiores ou igual a n₀.

Desta forma, está provado que, de fato, 5n²-n-3 = Ω(n²).

Resolução matemática: 3º exemplo (errado)

Vamos tentar demonstrar pela definição que 2n+1=Ω(n²).

Primeiramente, temos que:

• f(n) = 2n+1
• g(n) = n²

Se, pela definição matemática, precisamos demonstrar que existe uma constante positiva c e um valor positivo n₀ inicial, de forma que:

• f(n) ≥ c.g(n) para todos os n ≥ n₀

Então, para este problema, precisamos mostrar que:

• 2n+1 ≥ c.n² para todos os n ≥ n₀

Em suma: precisamos provar que, para todos os valores de n maiores ou igual a n₀, a função 2n+1 é maior ou igual a c multiplicado por n².

À primeira vista, percebe-se que 2n+1 possui comportamento linear e c.n² possui comportamento quadrático. Desta forma, percebe-se que essa demonstração é falsa, pois uma função quadrática (c.n²) não pode representar um limite assintótico inferior para uma função linear (2n+1).

No entanto, vamos realizar uma análise mais aprofundada para perceber o motivo dessa impossibilidade.

Vamos realizar algumas transformações algébricas no âmbito de isolar a constante c na inequação e perceber os seus possíveis valores:

A inequação resultante já nos mostra a impossibilidade de existir alguma constante c que a torne válida para grandes valores de n (n→∞), pois, independentemente do quão grande for o valor de c, o denominador n² sempre irá tornar o resultado da função cada vez menor.

Observe na tabela abaixo como o valor da função fica cada vez menor quando comparado com o valor de c (considerando c=1, que é o seu valor mínimo). Pode-se perceber que os valores da função se aproximam de zero ao passo que o valor de n cresce.

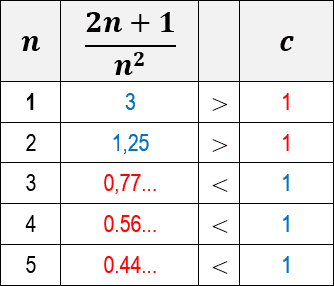
Isso significa que, mesmo com o menor valor possível para a constante c, a função sempre irá diminuir a ponto de se tornar menor que a constante.

Portanto, não conseguimos demonstrar o nosso objetivo. Não existe uma constante c e um n₀, tal que 2n+1 ≥ c.n² para todos os valores de n maiores ou igual a n₀.

Desta forma, está provado que, de fato, 2n+1≠Ω(n²) (lê-se “não é Ômega de n ao quadrado”).

Exercícios

Para demonstrar que você compreendeu bem o conceito e a definição matemática formal da notação Big Ômega, resolva os exercícios propostos:

Exercícios A

Tente demonstrar matematicamente que n²+800 = Ω(n).

Tente demonstrar matematicamente que 2n+10 = Ω(n).

Tente demonstrar matematicamente que n+10 = Ω(n²).

Tente demonstrar matematicamente que 7n-2 = Ω(1).

Tente demonstrar matematicamente que n²+20n+5 = Ω(n³).

Exercício B

Utilizando a técnica de contagem de instruções, encontre a fórmula de complexidade T(n) do algoritmo abaixo e, em seguida, tente demonstrar matematicamente que essa fórmula encontrada é Ω(n²).

1.public static void func(int[ ] n){
2.    for (int i=0; i<n.length-1; i++) {
3.        n[i]=i+i;
4.    }
5.}

Continue os seus estudos neste curso e leia o próximo artigo sobre a última de três notações usadas na computação para representar o comportamento assintótico dos algoritmos: a “notação Theta”.