Somatórios: o que são?

Introdução

O somatório é uma simbologia matemática usada para representar somas sucessivas de termos em uma sequência. Ele é comumente utilizado para representar fórmulas e expressões que envolvem somas sucessivas de elementos, tal como a média aritmética e as fórmulas usadas na área da estatística.

Até o final deste artigo, lhe apresentaremos não só a definição de somatórios, mas também vários exemplos que mostram na prática como funciona a sua representação.

Definição da simbologia de Somatório

Essa notação matemática utiliza a letra grega ∑ (Sigma) e permite reduzir o tamanho da representação de uma longa soma a uma única expressão. Veja o exemplo abaixo:

3+4+5+6+7+8+9+10+11+12+13+14

Uma looooonga expressão de soma

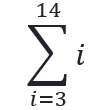
Pode ser representada como um somatório

Viu só como, por definição, o conceito de somatório é bem simples?

Agora, vamos entender os elementos que compõem o corpo da simbologia do somatório. Ela é formada por alguns elementos pontuais.

Na parte superior temos o símbolo n, que representa o índice final da soma (até qual valor a soma vai ser realizada).

Na parte inferior temos o símbolo m, que representa o índice inicial da soma (a partir de qual valor a soma vai ser iniciada).

O i representa a variável que irá assumir todos os valores entre m e n, começando por m. Ex.:

Para um somatório cujos valores m e n são, respectivamente, 2 e 5

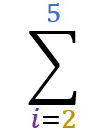
O simbolo i representará os valores 2,3,4,5 em cada etapa do somatório.

O símbolo t representa o termo do somatório. Representa o que será somado durante as etapas. O significado desse termo depende da fórmula e do uso do somatório. Veja alguns exemplos diversos para entender como o termo do somatório pode ser usado.

Índice como Termo do Somatório

O exemplo abaixo ilustra uma situação onde o termo é o próprio índice do somatório:

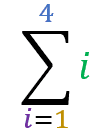
1+2+3+4 = 10

Perceba nessa situação que cada etapa do somatório nada mais é do que o próprio índice naquela etapa.

Valor constante como Termo do Somatório

O exemplo abaixo ilustra uma situação onde o termo é um valor constante:

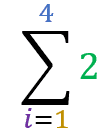
2+2+2+2 = 8

Perceba nessa situação que cada etapa do somatório nada mais é do que o valor 2. São quatro etapas (de 1 a 4) somando o único valor 2.

Função como Termo do Somatório

O exemplo abaixo mostra um uso mais sofisticado (e até mais útil) do somatório, onde o seu termo é uma função:

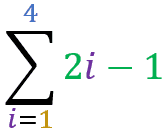
(2x1-1)+( 2x2-1)+( 2x3-1)+( 2x4-1) = 1+3+5+7 = 16

Perceba que cada etapa do somatório utiliza o valor do i e o substitui na função 2i – 1.

Agora que você “pegou a manha”, tente achar o resultado para os seguintes somatórios:

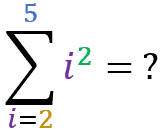
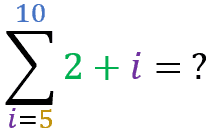
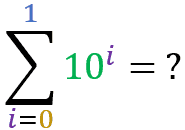
Somatório de elementos de conjuntos

O somatório também é utilizado para realizar somas de termos de um conjunto. Observe o seguinte exemplo:

Imagine um conjunto de sete valores X = { 10₁, 3₂, 5₃, 7₄, 2₅, 9₆, 4₇ }, onde o valor 10 é o elemento na posição 1, o 3 é o elemento na posição 2, em diante… Até o elemento 4 na posição 7. Podemos usar a notação de somatório para representar somas de elementos desse conjunto. Veja o exemplo:

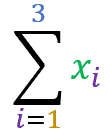
x₁+x₂+x₃ = 10+3+5 = 18

Este somatório indica que serão somados os 3 primeiros termos do conjunto X. O termo x_i indica que, em cada etapa, serão somados os elementos do conjunto X nas posições i.

Veja outro exemplo para o mesmo conjunto X = { 10₁, 3₂, 5₃, 7₄, 2₅, 9₆, 4₇ }:

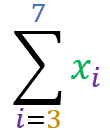
x₃+x₄+x₅+x₆+x₇ = 5+7+2+9+4 = 27

Este somatório indica que serão somados os elementos das posições 3, 4, 5, 6 e 7 do conjunto X.

Agora calcule você mesmo o resultado do somatório abaixo para o conjunto Y = { 100₁, 30₂, 20₃, 25₄, 2₅ }:

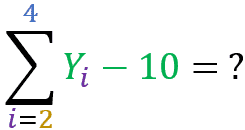
Viu como é bem fácil entender os somatórios? Aliás, qualquer assunto se torna fácil de aprender quando é explicado da maneira correta.

Entender os somatórios é apenas o primeiro passo. O que você precisa saber mesmo é como usar as propriedades dos somatórios, pois elas te permitirão resolver equações e problemas mais complexos.

Clique aqui e acesse o artigo onde nós te explicamos detalhadamente sobre as propriedades dos somatórios.