Logarithm properties
Learn about the Logarithm properties and learn how to use them to solve various types of algebraic operations.
11/09/2023
Introduction
Like many mathematical subjects, logarithms have properties that allow us to perform certain algebraic conversions as well as rewrite entire expressions. The purpose of logarithm properties is to simplify the resolution of difficult problems.
Before you can understand the logarithm properties you must be familiar with the concept. If you are unfamiliar with the concept of logarithm, click here and read the article where we explain you in detail about it.
Basic logarithm properties
Equivalence
The property states that:

If the logarithm of a number a in base b

is equals the logarithm of another number c in the same base b
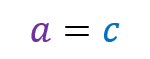
then a equals c
Logarithm of 1
The property states that:
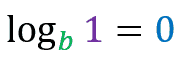
The logarithm of 1 in any base is always equal to 0(zero).
Let’s go to the demo:
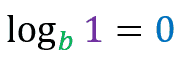
it is the same as
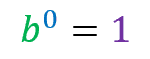
Which is true, because by the mathematical rule, any number raised to 0(zero) will always be equal to 1.
Logarithm of a in the base a
The property states that:
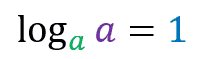
The logarithm of a number a on a base of the same value a is always equal to 1.
Let’s go to the demo:

it is the same as
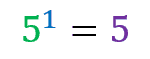
Which is obviously true!
Now it’s your turn:
Based on the basic logarithm properties, find the value of x in the equations below:
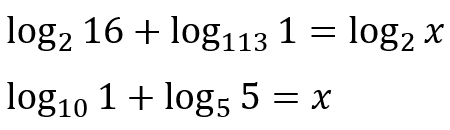
Operative logarithm properties
Logarithm of Product
The property states that:
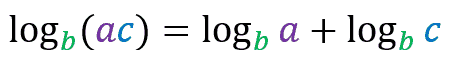
The logarithm of the product of two numbers a and c in a base b is always equal to the logarithm of the number a in base b plus the logarithm of the number c in base b.
Let’s go to the demo:

Logarithm of Quotient
The property states that:
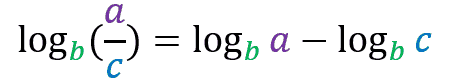
The logarithm of the quotient of two numbers a and c in a base b is always equal to the logarithm of the number a in base b minus the logarithm of the number c in base b.
Let’s go to the demo:
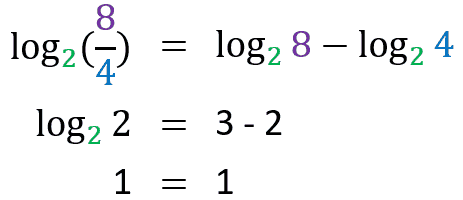
Logarithm of Power
The property states that:
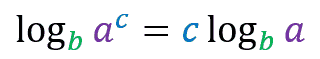
The logarithm of a number a raised to exponent c in base b is always equal to exponent c multiplied by the logarithm of number a in base b.
Let’s go to the demo:
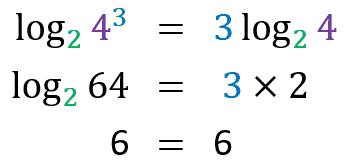
Now it’s your turn:
Based on the operative logarithm properties, find the value of x in the equations below:
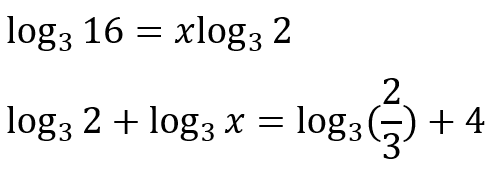
Advanced logarithm properties
Conversion to logarithm
The property states that:
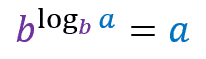
A number b raised to the logarithm of a number a in base b is equal to a.
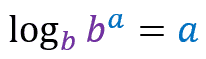
The property also states that the logarithm of ba in base b is equal to a.
Let’s go to the demo:
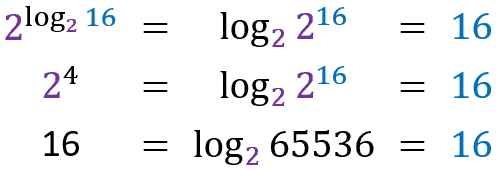
This is one of the most useful and interesting properties because it teaches us how to convert any number to a logarithmic representation. This allows us to solve many difficult expressions involving logarithms.
Change of base
The property states that:
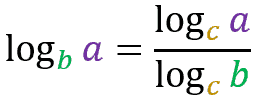
The logarithm of a number a in base b is equal to the logarithm of number a in a third base c over the logarithm of number b in that same third base c.
Let’s go to the demo:
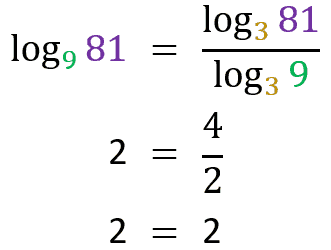
This is also a very important logarithm property because it teaches us how to convert a logarithm from one base to another logarithm from any other base. This allows us to simplify and solve many difficult equations.
Now it’s your turn:
Based on the advanced logarithm properties, find the value of x in the equations below:
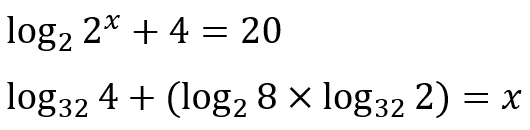
David Santiago
Master in Systems and Computing. Graduated in Information Systems. Professor of Programming Language, Algorithms, Data Structures and Development of Digital Games.