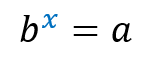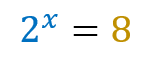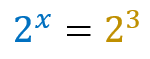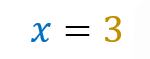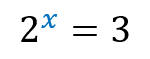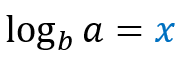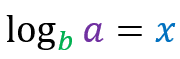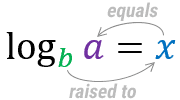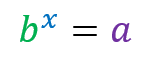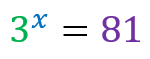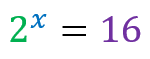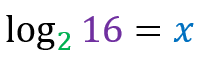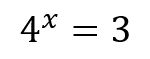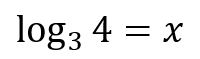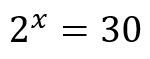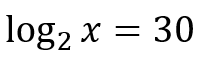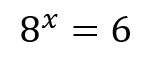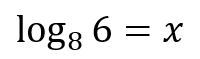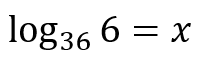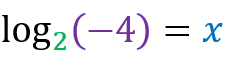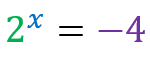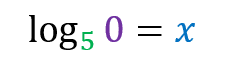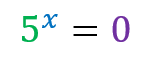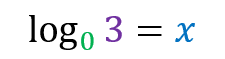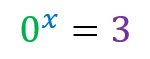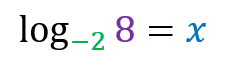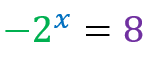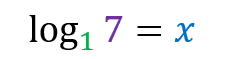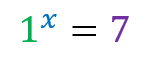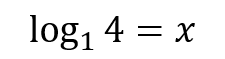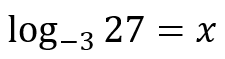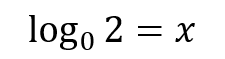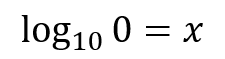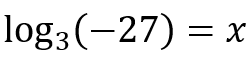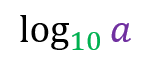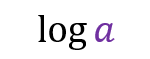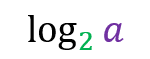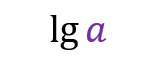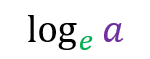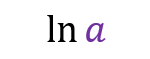More simply, we can understand logarithms as a mathematical symbology used to represent powers in a different way.
They arise from exponential equations, which are the equations that have the unknown in the exponent, of the following type:
Origin of Logarithms
To understand the origin of logarithms, let’s look at a property of exponential equations. The property that allows us to remove the unknown x from the exponent, reducing both sides of equality to the same base and then excluding the base. See the example:
To solve the equation: 2x = 8 we can factor the number 8 and represent it as 23. This way the equation could be represented as 2x = 23 and could be easily solved by excluding the bases (since they are equal), resulting in: x = 3.
Summing up:
Problem!
It turns out that there are certain situations in exponential equations where it is not possible to reduce both sides to the same basis! See the example:
Logarithms help solve these and other types of problems, where it is not possible to equalize the bases to remove the unknown from the exponent.
Definition of Logarithms
In the most summarized way possible, logarithms are just a mathematical symbology to represent an exponential function. Note:
Note in the illustration above that logarithm is a way of isolating the unknown x from the other side of equality. This facilitates many operations!
The structure of a logarithm has elements with very particular nomenclatures:
- Element b b is called the base.
- The x element is called a logarithm.
- Element a is the accented value.
Here’s how easy it is to convert a logarithm back to an exponential equation:
Here are examples of exponential equations converted to logarithms:
Now it’s your turn!
Answer true or false for the following exponential conversion proposals for logarithms:
Logarithms restrictions
Logarithms have certain restrictions that allow them to be mathematically valid and work in algebraic operations.
Given the logarithm:
The restrictions tell us that:
- The value of b must be positive and not equal to 1 (b > 0, b ≠ 1).
- The value of a must be positive (a > 0).
What is the reason for these restrictions? See some examples:
Unable to resolve because there is no exponent that raises the base 2 and results in -4.
Unable to resolve because there is no exponent that raises the base 5 and results in 0.
Unable to resolve because there is no exponent that raises the base 0 and results in a value greater than 1.
Unable to resolve because there is no exponent that raises the base -2 and results in 8.
Unable to resolve because there is no exponent that raises the base 1 and results in a value greater than 1
Now it’s your turn!
Based on the restrictions, show that the logarithms below are invalid.
Some conventions
In practical problem solving applications it is very common to use some conventions and generalizations for mathematical symbologies. With the logarithms is no different.
Decimal logarithms
When the logarithm base is 10, it is by convention to omit the base. e.g.
Binary logarithms
Widely used in computing, base 2 (or binary logarithms) are constantly used in their simplified form. Use the term lg instead of log and omit the base of the logarithm. e.g.
Natural logarithms
Another convention is that of natural logarithms (also known as neperians) which refers to logarithms in the base e (EULER number). e.g.
Understanding logarithms is just the first step. What you really need to know is how to use its properties, as they allow you to solve more complex equations and problems. Click here to access the article where we explain in detail the properties of the logarithms.